1. Алгебра
  2. Найдите: фактически, нужно

Найдите: фактически, нужно превратить дробь так, чтобы вместо х можно было подставить 1, и в знаменателе не получался 0. (т.к. на ноль делить нельзя)

golubinbogdab golubinbogdab    3   22.05.2019 23:20    1

Ответы
Soniadesor Soniadesor  18.06.2020 14:48
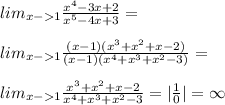lim_{x-1} \frac{x^4-3x+2}{x^5-4x+3}=\\\\lim_{x-1} \frac{(x-1)(x^3+x^2+x-2)}{(x-1)(x^4+x^3+x^2-3)}=\\\\lim_{x-1}\frac{x^3+x^2+x-2}{x^4+x^3+x^2-3}=|\frac{1}{0}|=\infty, так как неопределенности вида |0/0| или |\frac{\infty}{\infty}| нет, но если хочется поиграться, то
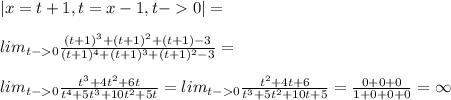|x=t+1,t=x-1, t-0|=\\\\lim_{t-0} \frac{(t+1)^3+(t+1)^2+(t+1)-3}{(t+1)^4+(t+1)^3+(t+1)^2-3}=\\\\lim_{t-0} \frac{t^3+4t^2+6t}{t^4+5t^3+10t^2+5t}=lim_{t-0} \frac{t^2+4t+6}{t^3+5t^2+10t+5}=\frac{0+0+0}{1+0+0+0}=\infty;
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
ьпоаь1 ьпоаь1  17.05.2021 13:23
Представьте в виде дроби. . ​...
Aрiшkа Aрiшkа  17.05.2021 13:23
Найдите общий вид первообразных для функции ​...
dashalev2510 dashalev2510  17.05.2021 13:23
А^3-3а^2/а^2-9 помагите добрые люди очень нужно ​...
toshaprostakis45 toshaprostakis45  17.05.2021 13:22
При каких значениях х значение квадратного трехчлена −2−+3 будет больше 1? Найдите целые решения неравенства...
Мама1мама2 Мама1мама2  17.05.2021 13:22
Интегралды эсептегилеf(5x4+2x-1)dx...
alina20041002 alina20041002  17.05.2021 13:22
Х^2+3х-1/х^2-49 добрые люди очень нужно ​...
Попорпо Попорпо  17.05.2021 13:22
A+b/x+a - a-b/x+a очень нужно ​...
nfz43616 nfz43616  17.05.2021 13:22
Упростить выражение (x/xy-y^2-y/x^2-xy)/x^2-y^2/8xy...
Акулинна Акулинна  17.05.2021 13:21
1) x²-xy/x²+xy×x²y+xy²/xy 2)(2x-y)²:4x³-xy²/33)n²-n⁴+n⁶/1-n×n²-1/n⁵-n³+n4)(x/x+1+1)×1+x/2x-15)x-2/x-3×(x+x/2-x) С ФОТКОЙ НУ ИЛИ ЖЕ БЕЗ ТОЧНЫЙ ПРАВИЛЬНЫЙ ОТВЕТ ​...
224678 224678  17.05.2021 13:21
1 вариант 6d-181. При каких значениях переменной, алгебраическая дробь(d-3)имеет смысл?45a3832. Сократите дробь :54a3с2 +4+43. Упростите дробь: и найдите значение дроби при c...

Популярные вопросы