Найдите cosα, если sinα = -4/5 и 3π\2 < α < 2π

Ответы

Elisavettas 10.08.2020 21:45

Так как α - угол четвёртой четверти, то Cosα > 0.

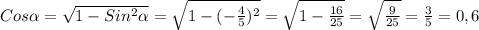
$Cos \alpha = \sqrt{1-Sin ^{2} \alpha } = \sqrt{1-( -\frac{4}{5}) ^{2}}= \sqrt{1- \frac{16}{25} } = \sqrt{ \frac{9}{25} }= \frac{3}{5}=0,6$

ПОКАЗАТЬ ОТВЕТЫ

ми34ми56 10.08.2020 21:45

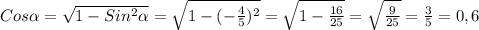
Cosa=√(1-sin²a)=√(1-16/25)=√(9/25)=3/5,a-в 4 четверти

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра

Sayva11 08.04.2020 14:55

Сколько корней имеет уравнение?...

milka0121 08.04.2020 14:55

памагит Решите систему уравнений графическим...

ЕкатеринкA 08.04.2020 14:55

Даны доходы Миши по месяцам. Вычисли амплитуду. 1. 11034 руб. 2. 12207 руб. 3. 12684 руб. 4. 13343 руб. 5. 13633 руб. 6. 14407 руб. 7. 14466 руб. 8. 15121 руб. 9. 15835...

Kozlovanika71 08.04.2020 14:55

Запишіть у вигляді звичайного дробу число 5,7(43)...

Avetodor 08.04.2020 14:54

Знайти шостий член і суму п яти перших членів геометричної прогресії (bn) , якщо b1=24, a q=14....

ALEXSEENKOALEX 08.04.2020 14:54

Найдите значение выражение 17^3-317^2*14+51*14^2-14^3 =...

akr999 08.04.2020 14:54

При яких натуральних значеннях n значення виразу число...

PAVELBOR 22.02.2021 20:21

с математикой. тригонометрия((...

nakjuo 22.02.2021 20:22

Если: 1)sinα = √3/3, тогда 1 - sinα cosα ctgα2) tgα = 2/3, тогда tgα + ctgα/tgα - ctgα3) tgα = 2/5, тогда sinα - cosα/sinα + cosα4) tgα = 3/2, тогда sinα cosα/sin²α - cos²α5)...

kremerartem1 16.06.2019 11:50

Найти функцию обратную данной х=4/(х-2) . и если можно с объяснением . ....

Найдите cosα, если sinα = -4/5 и 3π\2 < α < 2π

Популярные вопросы