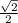Найдите cosα, если sinα=√2/2, 0<α<π/2

Другие вопросы по теме Алгебра
Популярные вопросы
- Всхемах уравнений расставьте коэффициенты , уравняйте : 1) li+o2= li2o 2) o2=o3...
3 - 1. как называется запись порядка аминокислот всех белков орга-ш низма, хранящаяся...
2 - Чистота,сказывать,масло,побелка,белить,звонить,сказка,масляный,белый,звонкий,звон,чистить,маслить,сказочный,чистый,звонок,чистенький,маслице....
2 - Одно основание трапеции на 6 см больше другого, а средняя линия равна 10 см....
1 - Найдите точку пересечения прямых: 2х-у=0 и х-3у=4...
2 - Для растворения 8,2 г смеси карбонатов кальция и магния в воде потребовалось...
3 - Что будет если яйцо в колу положить...
2 - Преобразуйте линейное уравнение с двумя переменными к виду линейной функции...
1 - Связь в оксиде серы so₃ 1. ковалентная полярная 2. ковалентная неполярная 3....
1 - Разбор слова превосходно по составу...
2
Объяснение:
Из основного тригонометрического тождества:
sin²α+cos²α=1
cos α =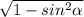
cos α =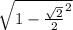
cos α =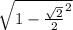
cos α =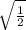
cos α = ± = ±
= ±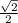
Т.к. α∈(0; π/2), то α - угол первой четверти, значит cos α >0 ⇒ cos α =