Найдите число n членов прогрессии у которой b2=1/8; b5=1/512; sn=85/128.
Ответы

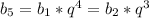
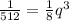 ⇒
⇒ 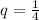

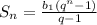 ⇒
⇒ 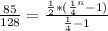
 ⇒
⇒  ⇒
⇒ 
Другие вопросы по теме Алгебра
Популярные вопросы
- Известно что в кодировке CP-1251 один символ занимает 1 байт. Определите...
2 - How often do you go to a café or a restaurant? What do you usually...
1 - 3. Закончите предложение 5% класса – это:A) десятая часть класса;...
1 - Жекпе жек какие инструменты использовались...
1 - 1. Какие из перечисленных ниже материалов можно подвергать неразрушающему...
2 - Найдите значение tgα , если cosα=-1/5 , αϵ III четверти...
2 - Какой энергией обладает яблоко (1) когда еще висит на дереве...
1 - Тест «Спряжение глаголов» 1. Продолжите: спряжение - это... А. изменение...
3 - Приведите примеры организмов схожих по систематической группе и организмов...
3 - Загадка она по небу к telolet в озёрах растопила землю всё теплом...
2