Найдите целую часть числа 1+1/sqrt(2) +1/sqrt(3) ++1/sqrt(256)

Для оценки снизу(что больше 30) мы берём интеграл функции 1/√х, т.е. 2√х. Возьмём его в промежутке от 256 до 1, значение равно 30(2*(√256-√1)) и является огранием снизу.(очевидно, что это ограничение именно снизу, т.к. сумма ряда-сумма площадей прямоугольников, содержащих в себе всю площадь интеграла)

Теперь найдём некоторую функцию, которая будет содержать в себе всю площадь этих самых прямоугольников:

Докажем, что 1/sqrt(2) +1/sqrt(3) +...+1/sqrt(256)<30. Возьмём функцию 1/√(х-1). В промежутке от х=2 до х=257 лежит целиком вся площадь рассмотриваемых прямоугольников. Т.е. интеграл этой функции на этом промежутке может служить верхней границей: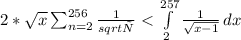 . Тогда его значение на промежутке равно 30(=2*(√(257-1)-√(2-1))), а т. к. границы площадей прямоугольников и функции не совпадают, но все прямоуг. лежат под графиком, то 1/sqrt(2) +1/sqrt(3) +...+1/sqrt(256)<30(строго меньше), а значит 1+1/sqrt(2) +1/sqrt(3) +...+1/sqrt(256)<31

Тогда, т.к. 30<1+1/sqrt(2) +1/sqrt(3) +...+1/sqrt(256)<31, то целая часть этого  ряда равна 30

ответ:30.

P.S. Площадью графика я называл площадь под графиком, которая считается равной значению определённого интеграла на этом участке.