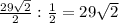Найдите боковую сторону ав трапеции авсd если углы abc и bcd равны соответственно 30° и 135° а cd=29
надюша5056
2
12.10.2019 21:54
1
Другие вопросы по теме Алгебра
ARCrafter
27.04.2020 12:47
uhjvjvjkybz
27.04.2020 12:47
ЦаринаПятёрок
27.04.2020 12:47
Аиляра
27.04.2020 12:47
vlad1458
27.04.2020 12:47
mukola11
27.04.2020 12:47
DenisYTYT
27.04.2020 12:47
zeynab97
12.09.2019 09:20
Kintavr12345
12.09.2019 09:20
Популярные вопросы
- складіть рівняння реакції між натрій сульфітом і йрдидною кислотою. Запишіть...
2 - У рівнобічнох трапеції ABCD снови дорівнюють 12 і 18 см. Висота AH дорівнює...
3 - Яким богам поклонялись давнi римляни?...
2 - Характеристика образу Халіни шоколад з чилі...
1 - Кто ответит не по теме - тому БАН. Напишіть твір-опис картини Фотія Красицького...
2 - два візка масами 2 кг та 3 кг рухаються назустріч один одному, зі швидкостями...
1 - Речення зі словами: замість передмови, в місце призначення, в місце призначення,...
3 - Знайдіть площу паралелограма, сторони якого дорівнюють 9 см і 41 см,...
2 - Довести, що рівняннях? 4 у? К 4х - 8у - 5 - 0 є рівнянням кола. Знайти...
2 - решить Реши неравенство −(5d+8)+(d−11) 0.(В первое окошко запиши знак...
2
Объяснение:
В трапеции AD параллельно BC, угол BCD равен 135°, значит угол CDA равен 180-135=45°
CD=29, угол 45°, значит высота h трапеции равна:
29*sin(45°)=29*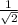
=
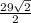
Зная высоту h трапеции и угол ABC, находим AB.
AB = h/sin(30°)=