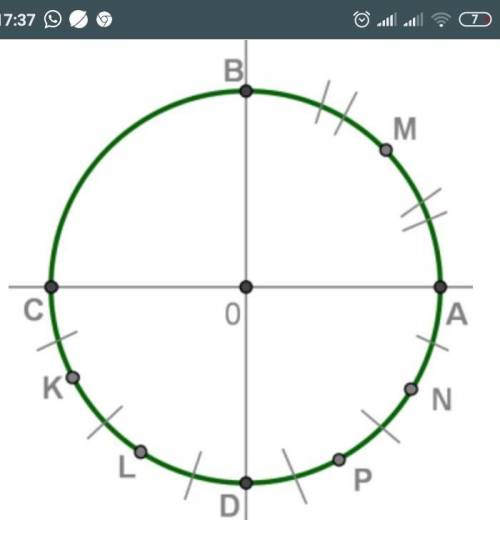
Найди все числа, которым соответствует на числовой окружности точка K. Выбери нужный вариант ответа. 1) 3π4+2πk,k∈Z
2) 2πk,k∈Z
3) 4π3+2πk,k∈Z
4) π2+2πk,k∈Z
5) π+2πk,k∈Z
6) π4+2πk,k∈Z
7) 3π4+2πk,k∈Z
8) 3π2+2πk,k∈Z
9) 2π3+2πk,k∈Z
10) 7π6+2πk,k∈Z
Другие вопросы по теме Алгебра
Популярные вопросы
- Построить искомое сечение трех фигур...
1 - Написать сообщения как предсказывают погоду 2 класс...
3 - Найдите наименьшее общее кратное чисел: 80 40 48...
2 - Пробка относится к: 1)проводящей ткани 2)покровной 3)образовательной 4)запасающей...
1 - За какое время поезд,отправляясь от станции с ускорением 0,4 м/с2, пройдет...
1 - Вычислите 308 умножить на 37 минус 29 умножить на 101 плюс 253 умножить на...
1 - На берегу моря был камень, на камне было написано роковое слово из 8 букв....
3 - Как вы думаете, какое значение имел переход к земледелию?...
2 - Какие углеводороды относят к циклоалканам и почему их так назвали? почему циклоалканы...
3 - Клубникисодержет 6% сахара сколькокг соджержет сахара в27кг клубники...
1
Для этого нужно взглянуть на числовую окружность и определить, какие точки соответствуют данной точке K.
Из задания мы видим, что K находится на окружности и равноудалена от точек 0 и -36. Из рисунка можно сделать вывод, что она находится примерно посередине между двумя этими точками.
Точка 0 соответствует углу 0 радиан (или 2π), а точка -36 соответствует углу -π/6 радиан (или -π/6 + 2π).
Точка K находится посередине между этими двумя углами. Значит, угол, соответствующий точке K, будет равен среднему значению этих двух углов.
Среднее значение между двумя углами θ₁ и θ₂ можно найти, сложив эти два угла и разделив результат на 2. В данном случае у нас есть угол 0 радиан и угол -π/6 радиан:
θ = (0 + (-π/6 + 2π))/2
= (-π/6 + 2π)/2
= -π/12 + π
= (π - π/12)
= 11π/12
Итак, угол, соответствующий точке K на числовой окружности, равен 11π/12.
Теперь, чтобы найти все числа, которым соответствует точка K на числовой окружности, нужно умножить 11π/12 на целое число k, где k - любое целое число. Это объясняет, почему в каждом из предложенных вариантов ответа есть 2πk, где k ∈ Z (Z обозначает множество всех целых чисел).
Таким образом, правильный вариант ответа на данный вопрос будет 2πk + 11π/12, где k ∈ Z.
Ответ: 2πk + 11π/12, где k ∈ Z.