Найди производную функций: a)2sinx/2-sinx
Ответы
Формулы :
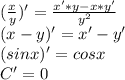
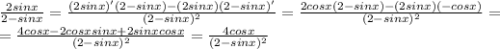
ПОКАЗАТЬ ОТВЕТЫ
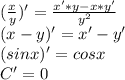
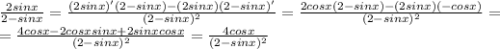
Другие вопросы по теме Алгебра
Популярные вопросы
- 2-мәтін) Қазақ халқы үшін төрт түліктің осалы жоқ. Дегенмен,...
1 - Прикладом пристосування що утворилося в результаті коеволюції...
3 - Хто знає фізику?До іть будь ласка, дуже ...
1 - в России каждый человек потребляет Ежедневно в среднем около...
3 - Cкласти речення за схемою [], (бо), і [] (якщо), (якщо), (якщо)...
3 - 10. Сүрөттөгү дары-дармектер жөнүндө эмнелерди билесиңер? МУКАЛТИНПЕРТҮССИЯEPTYGERТермопсолтаблетки...
2 - Точку A (5/3)і точку B що має протилежну координату іть!...
1 - Важное условие оплодотворения у споровых растений...
1 - мама готовит 100 шелпеклв за 30 минут сестра такие же 100 шелпеков...
2 - Help with English please Work in pairs. Complete the table about...
1