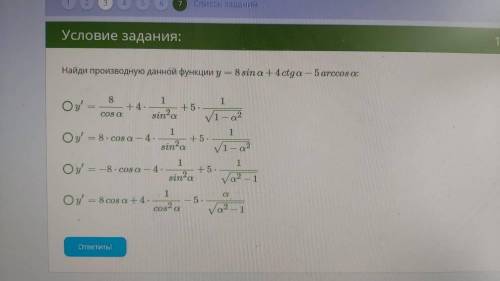
Найди производную данной функции y=8sinα+4ctgα−5arccosα: 1 y′=8cosα+4⋅1sin2α+5⋅11−α2−−−−−√
2 y′=8⋅cosα−4⋅1sin2α+5⋅11−α2−−−−−√
3 y′=−8⋅cosα−4⋅1sin2α+5⋅1α2−1−−−−−√
4 y′=8cosα+4⋅1cos2α−5⋅αα2−1−−−−−√

НАДО РЕШИТЬ!

Найди производную данной функции y=8sinα+4ctgα−5arccosα: 1 y′=8cosα+4⋅1sin2α+5⋅11−α2−−−−−√ 2 y′=8⋅co

Ответы

beksedaniar 28.03.2021 13:00

$y = 8 \sin( \alpha ) + 4ctg \alpha - 5arccos \alpha$

$y' = 8 \cos( \alpha ) - \frac{4}{ \sin {}^{2} ( \alpha ) } + \frac{5}{ \sqrt{1 - { \alpha }^{2} } } \\$

ответ: второй

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра

Fazzika 06.06.2019 21:20

дэнчик60 06.06.2019 21:20

liliakolokol 06.06.2019 21:20

schooll13 06.06.2019 21:20

jockman 08.11.2020 21:58

|x-a| B b 0Записать системой неравенств...

alexey2ristp00z7s 08.11.2020 21:57

tolodono 08.11.2020 21:57

maksimprikhodko 08.11.2020 21:56

yagyaevaremziep0dlir 04.08.2019 05:00

Вычислить - cos в квадрате75 ° - sin в кварате 75°...

ильюхха 04.08.2019 05:00