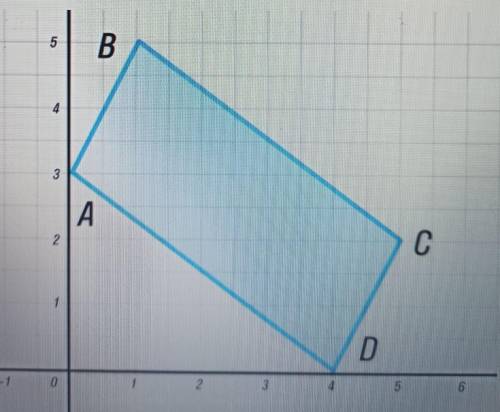
Найди площадь фигуры на координатной плоскости​

3,4 это же легко вы че

Объяснение:

Это же легко вы че

Привет! Я могу помочь тебе решить эту задачу. Давай начнем с того, что разберемся, как выглядит данная фигура на координатной плоскости.

Мы видим, что эта фигура состоит из трех различных фигур: прямоугольника, треугольника и полукруга.

1. Прямоугольник:
Сначала найдем площадь прямоугольника. Для этого нужно знать длину и ширину прямоугольника. Нам дано, что длина прямоугольника равна 8 единицам, а ширина равна 4 единицам. Площадь прямоугольника вычисляется по формуле: S = длина * ширина.
Заменяя значения в формуле, получаем S = 8 * 4 = 32.

Таким образом, площадь прямоугольника равна 32 квадратным единицам.

2. Треугольник:
Далее, нужно найти площадь треугольника. Для этого нужно знать основание и высоту треугольника. Нам дано, что основание треугольника равно 8 единицам, а высота равна 4 единицам. Площадь треугольника вычисляется по формуле: S = (основание * высота) / 2.
Заменяя значения в формуле, получаем S = (8 * 4) / 2 = 16.

Таким образом, площадь треугольника равна 16 квадратным единицам.

3. Полукруг:
Наконец, нужно найти площадь полукруга. Для этого нужно знать радиус полукруга. Половина длины прямоугольника является радиусом полукруга. Мы уже выяснили, что длина прямоугольника равна 8 единицам, поэтому радиус полукруга будет равен 8 / 2 = 4 единицы.
Площадь полукруга вычисляется по формуле: S = π * (радиус^2) / 2.
Значение π (пи) можно принять приближенно равным 3,14. Заменяя значения в формуле, получаем S = 3,14 * (4^2) / 2 = 3,14 * 16 / 2 = 3,14 * 8 = 25,12.

Таким образом, площадь полукруга равна примерно 25,12 квадратных единиц.

Теперь, чтобы найти общую площадь всей фигуры, нужно сложить площади всех трех фигур: 32 + 16 + 25,12 = 73,12.

Таким образом, общая площадь фигуры на координатной плоскости равна примерно 73,12 квадратных единиц.

Надеюсь, это решение помогло тебе понять, как найти площадь данной фигуры на координатной плоскости. Если у тебя возникнут еще вопросы или ты нуждаешься в дополнительной помощи, не стесняйся задавать их!