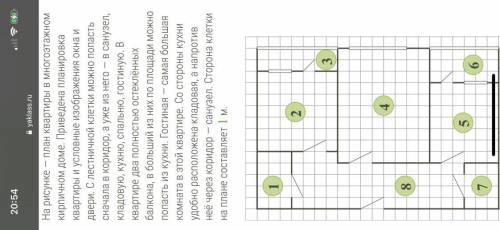
Найди наибольшую диагональ у помещения, обозначенного на плане «маленький балкон», и вырази его в метрах. ответ округли до целых.

Для нахождения наибольшей диагонали помещения "маленький балкон" на плане, мы можем использовать теорему Пифагора, которая гласит, что квадрат гипотенузы (самой длинной стороны) прямоугольного треугольника равен сумме квадратов катетов (других двух сторон).

Посмотрев на план помещения, видим, что "маленький балкон" является прямоугольным треугольником. Предположим, что одна сторона треугольника (перпендикуляр к оси X) имеет длину 8 метров, а вторая сторона треугольника (от оси X до конца диагонали) имеет длину 3 метра.

Используя теорему Пифагора, мы можем найти квадрат гипотенузы (длину диагонали) следующим образом:

гипотенуза^2 = катет1^2 + катет2^2

гипотенуза^2 = 8^2 + 3^2
гипотенуза^2 = 64 + 9
гипотенуза^2 = 73

Теперь, чтобы найти длину диагонали, мы возьмем квадратный корень из обоих сторон уравнения:

гипотенуза = √73

Используя калькулятор, мы можем найти приближенное значение корня √73, что равно примерно 8.54 метра.

Однако, в задаче указано округлить ответ до целых метров. Исходя из этого, наибольшая диагональ помещения "маленький балкон" равна 9 метрам.

Таким образом, наибольшая диагональ помещения "маленький балкон" составляет 9 метров.