1. Алгебра
  2. найди два натуральных числа

найди два натуральных числа если их среднее арифмитеческое равно 35 а среднее геометрическое равно 28​

miloradovich04 miloradovich04    1   14.09.2020 15:53    7

Ответы
assija56 assija56  15.10.2020 21:12

Объяснение:

Обозначим эти числа a и b.      ⇒

\left \{ {{\frac{a+b}{2}=35\ |*2 } \atop {\sqrt{a*b}=28 }} \right.\ \ \ \ \left \{ {{a+b=70} \atop {(\sqrt{a*b})^2=28^2 }} \right. \ \ \ \ \left \{ {{b=70-a} \atop {a*b=784}} \right.\ \ \ \ \left \{ {{b=70-a} \atop {a*(70-a)=784}} \right. \ \ \ \ \left \{ {{b=70-a} \atop {70a-a^2=784}} \right. \\ a^2-70a+784=0\\D=1764\ \ \ \ \sqrt{D}=42\\ a_1=14 \ \ \ \ \Rightarrow\ \ \ \ b_1=56\\a_2=56\ \ \ \ \Rightarrow\ \ \ \ b_2=14.

ответ: 14 и 56.


найди два натуральных числа если их среднее арифмитеческое равно 35 а среднее геометрическое равно 2
ПОКАЗАТЬ ОТВЕТЫ
seredinavi seredinavi  15.10.2020 21:12

Найдите два натуральных числа, если их среднее арифметическое равно 35, а среднее геометрическое равно 28.​

Среднее арифметическое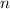 n чисел — сумма этих чисел, деленное на количество слагаемых:

\overline{x} = \dfrac{x_{1} + x_{2} + ... + x_{n}}{n}

Среднее геометрическое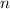 n чисел — арифметический корень 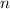n-ой степени из произведения этих чисел:

\sigma = \sqrt[n]{x_{1}\cdot x_{2} \cdot ... \cdot x_{n}}

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Interworm Interworm  02.06.2019 18:30
Сумма восьмого и шестого члена арифметической прогрессии равна 16, произведение второго и двенадцатого равно -36. найти разность и первый член...
влад2317 влад2317  02.06.2019 18:30
Разложите на множители y(a-b)+2(a-b)=...
Фарук11 Фарук11  02.06.2019 18:30
Докажите тождество a(a-2)-8=(a+2)(a-4)...
exm0r3d exm0r3d  02.06.2019 18:30
Решить уравнение 3/х-3/х+4=1(четыре тоже под дробью)...
ti0013 ti0013  02.06.2019 18:30
1.найдите первый член и знаменатель прогрессии если b3=1/6, b9=1/48 2. надите номер члена прогрессии в которой b1=3, q=2/3, bn=32/81...
arsenfedorko arsenfedorko  02.06.2019 18:30
Представить в виде многочлена (x+7)×(x-2)= (4с-b)(6c+3b)= (y+5)(y²-3y+8)=...
irinakotik17 irinakotik17  02.06.2019 18:30
Представить в виде многочлена (x+7)×(x-2)=...
Jeka990 Jeka990  21.09.2019 06:20
Градусная мера одного из углов с соответственными параллельными сторонами больше другого на 25 процентов.найдите разность кубов градусных мер этих углов. 30 ....
адам121 адам121  21.09.2019 06:20
Найдите координаты вершины параболы y=(x+2)^2 и постройте её график...
артем1151 артем1151  21.09.2019 06:20
Преобразуйте произведение в многочлен -3m(-2m²n+3m²+4mn²) сразу ответ.запишите ответ в виде многочлена или одночлена (например, выражение 2x²-3² запишите так 2x^2-3^2....

Популярные вопросы