Найдем область определения выражения 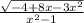

Другие вопросы по теме Алгебра
Популярные вопросы
- Найдите знаменатель бесконечной геометрической прогрессии, если известно:...
1 - дайте ответ! Сопоставьте произведения Н.В.Гоголя Шинель и Ф.М.Достаевского...
2 - с) Вставьте пропущенные термины В гуморальном иммунитете участвуют клетки...
2 - 1.Вычислить если возможно. а)б)в)г)д)е)2.Составить таблицу значений для...
2 - Астана болашақ қаласы тақырыбына термин ,неологизм сөздерді қолданып,эссе...
3 - Между числами -13,5 и 3,5 вставьте 3 чисел так, чтобы они вместе с данными...
2 - Учитель записал на доске три утверждения, относящиеся к молекулам 1. Размерами...
3 - Контрольная работа по разделу «Основы логики». Информатика...
1 - 4. Чему равна плотность жидкости, 25 л которой имеют массу 25 кг? Решение...
3 - AD=AE Использвов-AD=AE ,∆CAD=∆BAE , Докажите что BD=CE...
1
х€[2/3;1)U(1;2]
Объяснение:
1. Данное выражение неопределено при значениях х, обращающих его знаменатель в 0. Найду нули знаменателя:
х^2-1=0; х1=1, х2=-1
2. Данное выражение не определено, если подкоренное выражение отрицательно. Найду область определения:
-4+8х-3х^2>=0,
3х^2-8х+4<=0, Найду нули:
3х^2-8х+4=0, D=4^2-3×4=4,
x1=(4+2)/3=2, x2=(4-2)/3=2/3
х€[2/3;2]-решение неравенства.
3. Первое и второе условия должны соблюдаться одновременно, значит:
х€[2/3;1)U(1;2]
D(f) = [2/3; 1) U (1; 2]
Объяснение:
для того, чтобы определить D(f), нужно разделить выражение и рассмотреть каждый случай отдельно.
1. 1) нули функции
x² - 1 ≠ 0, откуда
x - 1 ≠ 0, x + 1 ≠ 0, x ≠ ± 1
отсюда: область определения: x ∈ R
2) - 4 + 8x - 3x²
-3x² + 8x - 4 ⩾ 0
3x² - 8x + 4 ⩾ 0
D = 64 - 12 × 4 = 16
x1 =
x1 =
x2 =
x2 = 2
x ∈ [2; +∞) U [2/3; +∞)
2. находим пересечение, необходимое, чтобы функция соблюдалась:
1) x ∈ (1; +∞) U [2; +∞)
x ∈ (1; 2]
2) x ∈ (1; +∞) U [2/3; +∞)
x ∈ [2/3; 1)