Натуральные числа 9n+2 и 5n-4 делятся на натуральное число m не равное 1. найти число m

Поскольку числа 9n+2 и 5n-4 делятся на натуральное число m, то и число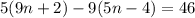 должно делится на m. И делится лишь в том случае, когда m = 1, m = 2, m = 23 и m = 46. Но число m = 1 не удовлетворяет условию

Пример таких чисел:

n = 2:             9n + 2 = 9 * 2 + 2 =20

                     5n - 4 = 5 * 2 - 4 = 6

Оба числа делятся на число m = 2.

n = 10:            9n + 2 = 9 * 10 + 2 = 92

                     5n - 4 = 5 * 10 - 4 = 46

Оба числа делятся на число m = 23 и m = 46.

ответ: 2; 23; 46.