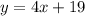Напишите уравнение касательной к графику функции 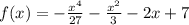 в точке этого графика с абсциссой x0= -3
в точке этого графика с абсциссой x0= -3
Другие вопросы по теме Алгебра
Популярные вопросы
- Как проверить слово замерзшая, если я сделала ошибку во второй з...
2 - Составьте предложение с обособленным приложением присоеденяющимся словами...
3 - Касса, парашют, фавна, медальон. что они обозначают ....
1 - Старший брат покрасил7/10забора а младший-1/4какая часть забора осталось...
2 - Составить предложение со словами километр, портфель, библиотека, каталог,...
3 - Выписать 5 пословиц, которые характеризуют страх с позитивной точки....
3 - Сколько килограммов сахара в 6 кг 40%-ного сахарного сиропа?...
1 - Вкаком предложении есть глагол в форме 1 лица множественного числа настоящего...
2 - Из пункта а в пункт в расстояние между которыми равно 240км одновременно...
3 - Напишите вопросы! пример; may l eat your apple? yes,you may eat my apple....
2
Объяснение:
В точке касания у графика и касательной совпадают значения функции и значения её производной.
Пусть касательная имеет вид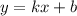 , тогда
, тогда 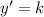
Таким образом получили уравнение касательной