1. Алгебра
  2. Напишите решение к неравенствам

Напишите решение к неравенствам

Logikahaha Logikahaha    3   12.10.2019 13:04    1

Ответы
akimkryt42 akimkryt42  10.10.2020 06:11

№1

\frac{(x+3)(x-3)^2(x-8)}{(x+2)^3(x-5)} \leq 0

находим корни числителя и знаменателя:

x_1=-3;\ x_2=3;\ x_3=8;\ x_4=-2;\ x_5=5

(x-3)^2 - всегда принимает неотрицательные значения. Значит при переходе через точку 3 неравенство знак не поменяет.

Используем метод интервалов:

точки (-2) и 5 - выколотые.

   +            -            +          +            -              +

-------[-3]--------(-2)-------[3]--------(5)--------[8]---------->x

x\in [-3;-2)\cup (5;8] \cup \{ 3 \}

ответ: x\in [-3;-2)\cup (5;8] \cup \{ 3 \}

№2

\frac{2x+12}{x-4} -1\leq \frac{5}{x+1}\\\frac{2x+12-x+4}{x-4} \leq \frac{5}{x+1}\\\frac{x+16}{x-4}- \frac{5}{x+1} \leq 0\\\frac{(x+1)(x+16)-5(x-4)}{(x-4)(x+1)} \leq 0\\\frac{x^2+12x+36}{(x-4)(x+1)} \leq 0\\\frac{(x+6)^2}{(x-4)(x+1)} \leq 0\\x_1=-6;\ x_2=4;\ x_3=-1

точки (-1) и 4 - выколотые

 +            +         -          +

------[-6]------(-1)------(4)------->x

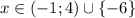
x\in (-1;4)\cup \{-6\}

ответ: x\in (-1;4)\cup \{-6\}

№3

замена:

y=x^2

получим:

y^2-5y+6\geq 0\\D=25-24=1\\y_1=\frac{5+1}{2}=3\\y_2=\frac{5-1}{2}=2\\y^2-5y+6=(y-2)(y-3)

обратная замена:

(x^2-2)(x^2-3)\geq 0\\(x-\sqrt{2})(x+\sqrt{2})(x+\sqrt{3})(x-\sqrt{3})\geq 0\\x_{1,2}=\pm \sqrt{2};\ x_{3,4}=\pm \sqrt{3}

  +              -                +              -               +

-------[-√3]-------[-√2]--------[√2]-------[√3]-------->x

x\in (-\infty;-\sqrt{3}]\cup [-\sqrt{2};\sqrt{2}]\cup [\sqrt{3};+\infty)

ответ: x\in (-\infty;-\sqrt{3}]\cup [-\sqrt{2};\sqrt{2}]\cup [\sqrt{3};+\infty)

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Alexgorila Alexgorila  13.11.2021 07:15
Исследуйте на монотонность последовательность (а n) ,заданную формулой :an=-3^n ; 2)an=5^n+1...
fgrtyrrrrty fgrtyrrrrty  13.11.2021 07:16
Какая из этий функций парная? 1) y=x^(3)-x 2) y=x^4-23x^3 3) y=28x^5+3x^2 4) y=19x^2+23x^6...
andrstoyan182 andrstoyan182  21.04.2020 12:57
Не строя график, определить, при каком значении х функция принимает наибольшее и наименьшее значение, если y=-3x^2+12x-2​...
викуля1101 викуля1101  23.05.2019 23:30
Доказать что f(x)= -2x^2-x+3 возрастает на промежутке ( - бесконечность; 1/4)...
emmka1 emmka1  23.05.2019 23:30
Может ли сумма квадратов двух последовательных натуральных чисел равняться сумме кубов трех последовательных натуральных чисел ?...
Sofi432432 Sofi432432  23.05.2019 23:30
1. сторона ромба равна 90, острый угол 30. найдите радиус вписанной окружности ромба. 2. найдите площадь круга, вписанный в равносторонний треугольник со стороной...
Xtarlus Xtarlus  23.05.2019 23:30
Будьте добры найдите значение переменной,при которых не имеет смысла выражение: а) 2x-x(в квадрате) x+7 б) 1-x |x|+1,5 в)55 2|x|-5 г) x(в квадрате)-1 x(в квадрате)+1...
udovilyudmila udovilyudmila  23.05.2019 23:30
За 7-8 класс сделайте все с решением ) можно не все но побольше главное ) №1.найдите произведение корней уравнения: 2x^2-4x-70=0 №.2 найдите сумму корней уравнения:...
Салатикус Салатикус  23.05.2019 23:30
Как без построения графиков функции определить взаимное расположение точек на координатной плоскости?...
ппмв ппмв  23.05.2019 23:30
Який відсоток вмісту солі в розчині, якщо в 400гр. міститься 14г солі...

Популярные вопросы