Напишите несколько лёгких решений и вычисления этого выражения: 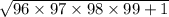
без использования калькулятора.
Другие вопросы по теме Алгебра
Популярные вопросы
- Как решить за первый час было расчищено 5 семнадцатых всей дороги...
2 - Вмагазине продали 144 кг ягод .2/6 этих ягод составляет смородина 3/8-клубника...
2 - Жилина и костылина например : : дабрый злай и тд...
1 - Написать маленькое сообщение о священном животном в древнем египте-скарабей. только...
1 - Десятый, второй, пятый,первый это прилагательные?...
2 - Как называются теоремы,обратные признакам параллельности прямых?...
3 - Вмагазине продали 124 магнитофона по цене 875 руб сколько денег выручил магазин...
3 - Сообщение про любую обязанность гражданина россии...
2 - Периметр прямоугольника с длиной 9 см и шириной 6 см можно найти с выражения 1)...
2 - 50 .придумать текст на о семье 6-7 предложений! !...
2
ответ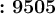
Объяснение:
Сделаем замену :
Для решения таких задач стоит запомнить формулу :