1. Алгебра
  2. Написать уравнение касательной

Написать уравнение касательной и нормали к кривой x^3+y^2+2x-6 в точке с ординатой y0=3

nadyushasukhan nadyushasukhan    3   30.09.2019 04:40    5

Ответы
Толик566 Толик566  09.10.2020 04:38

Касательная - прямая, которая касается к кривой в точке (x₀;3), где x₀ - абсцисса касания. Подставим координаты точки касания в заданное уравнение кривой

x_0^3+3^2+2x_0-6=0\\x_0^3+2x_0+3=0

Путем подбора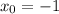 x_0=-1, уравнение имеет единственный корень, так как функция, соответствующая данному уравнению, является монотонной.

(-1;3) - точка касания касательной.


\displaystyle \frac{\partial y}{\partial x}=-\frac{\cfrac{\partial}{\partial x}\left(x^3+y^2+2x-6\right)}{\cfrac{\partial}{\partial y}\left(x^3+y^2+2x-6\right)}=-\frac{3x^2+2}{2y}

Найдем теперь значение производной в точке (-1;3).

\displaystyle \frac{\partial}{\partial x}f(-1;3)=-\frac{3\cdot (-1)^2+2}{2\cdot 3}=-\frac{5}{6}

Уравнение касательной к кривой:

\displaystyle F(x)=y_0+y'(x_0)(x-x_0)=3-\frac{5}{6}\cdot \left(x+1\right)=\frac{-5x}{6}+\frac{13}{6}


Уравнение нормали к кривой:

\displaystyle F_n=y_0-\frac{x-x_0}{y'(x_0)}=3-\frac{x+1}{-\cfrac{5}{6}}=\frac{6x}{5}+\frac{21}{5}

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
AnnaKor14 AnnaKor14  06.12.2020 10:16
Алгебра 7 класс!! Даны три уравнения: 1) 11х - у =17, 2) х + 11у =17, 3) 7х + у =1. Из каких двух уравнений можно составить систему, чтобы её можно было сразу начать решать...
Bananthic Bananthic  06.12.2020 10:16
11 0Хk=0; b 0k=0: b 0k 0; b=0 0; b 0k 0:b 0туk 0; b=0k 0: b=0k 0:b 0Сохранить в АИСИх упралне​...
sanadakim sanadakim  06.12.2020 10:17
найти какие значение может принимать и f(x)?​...
MafiiMan7204720 MafiiMan7204720  06.12.2020 10:18
Нужно решить 1,2,4 Могу еще денег докинуть на сбер...
Masha6996 Masha6996  06.12.2020 10:19
Решите уравнение : \frac{x-14}{5}-\frac{6x-45}{7}=1[/tex] (Это всё в дробях!) ооочень Мне нужен не только ответ но и по шаговое решение!...
kedr3 kedr3  06.12.2020 10:21
Сравните числа (с решением): 1 5\13 ... 1, (39) смотрите картинку ниже (там более точно показано):...
маг122 маг122  29.09.2019 02:40
Как найти порядок числа? порядок числа a равен12, а порядок числаb равен14 . каким может быть порядок частного b/a...
coolplayer1 coolplayer1  29.09.2019 02:40
А)3*(8а-4)+6а б)11с+5*(8-с) в)2*(у-1)-2у+12 г)16+3*(2-3у)+88 а)7р-2*(3р-1) б)-4*(3а+2)+8 в)3-17а-11*(2а-3) г)15-5*(1-а)-6а...
pekus228 pekus228  29.09.2019 02:40
Доказать,что n(2n-1)(2n+1) кратно 3...
rortat32 rortat32  29.09.2019 02:40
Функция задана формулой y=-4/x. 1)найдите значение функции , если значение аргумента равно -1; 4. 2)найдите значение аргумента , если значение функции равно -4; 2....

Популярные вопросы