надо решить прогрессию.нам дано: q=3, bn=567, sn=847.найти b1=? , n=?
Другие вопросы по теме Алгебра
Популярные вопросы
- Заповніть таблицю: «Родина афінянина» обов язки чоловіка Обов язки...
3 - На рисунке AE и CD - медианы треугольника ABC, OE = 4 см. Найдите...
3 - Мужчины и женщины 1. Выберите верные суждения. 1) Понятия «гендер»...
3 - 1-и работник выполнил работу за 10 дней, 2-ой за 15 дней. За сколько...
3 - Рассчитайте pH раствора, образующегося при сливании 250 мл соляной...
2 - Чи існую трикутник зі сторонами : 1) 5 см,9 см, 14 см; 2) 6 см,...
3 - 12. Прочитайте. Вставьте пропущенные буквы. Над именами прилагательными...
3 - 3 КЛАСС И ПОСТАВЛЮ КАК ЛУЧШИЙ ОТВЕТ....
1 - Какое значение питательных веществ для растений !...
3 - ответьте на все вопросы Аналізуємо твір Костянтина Симонова «Жди...
1
ответ: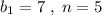 .
.
Объяснение: