На сколько изменится площадь квадрата, если одну сторону уменьшить в N раз, а вторую на 15%?

Question

Алгебра: На сколько изменится площадь квадрата, если одну сторону уменьшить в N раз, а вторую на 15%?

Aksiomsa868589 · Answer

Все стороны квадрата равны х . Площадь квадрата равна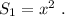 $S_1=x^2\ .$

Если сторона квадрата уменьшается в N раз , то она станет равной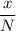 $\dfrac{x}{N}$ .

Если сторону квадрата уменьшить на 15%, то она станет равной

x-0,15x=0,85x .

Площадь фигуры , уже прямоугольника, равна

$S_2=\dfrac{x}{N}\cdot 0,85x=\dfrac{0,85}{N}\cdot x^2=\dfrac{0,85}{N}\cdot \cdt S_1$

Площадь уменьшится на

$S_1-S_2=S_1-\dfrac{0,85}{N}\cdot S_1=\Big(1-\dfrac{0,85}{N}\Big)\cdot S_1=\Big(1-\dfrac{17}{20\, N}\Big)\cdot S_1$