На сборку поступают детали с двух автоматов. первый дает в среднем 0,1% брака, а второй – 0,3% брака. на сборку поступило 2500 деталей с первого автомата и 2000 – со второго. найти вероятность того, что первая взятая деталь, оказавшаяся бракованной, была изготовлена первым автоматом. с полным решением

Пусть событие А — взятая деталь бракованная.

деталь изготовлена первым автоматом;

деталь изготовлена вторым автоматом;

Условные вероятности: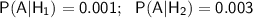

По формуле полной вероятности, вероятность того, что наугад взятая деталь бракованная, равна

По формуле Байеса, вероятность того, что взятая деталь была изготовлена первым автоматом, равна