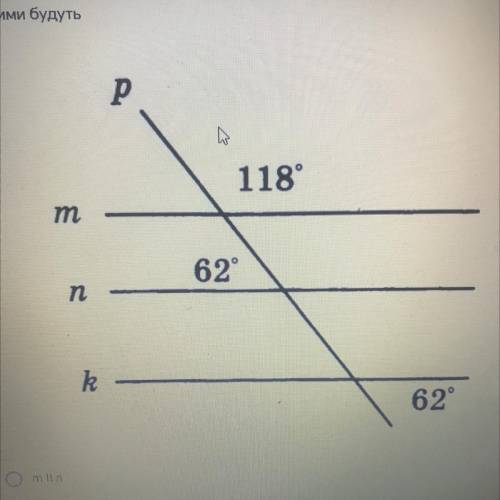
На рисунке прямые m, n, k пересекаются секущей р. Параллельными прямыми будут...

На рисунке видно, что секущая р пересекает прямые m, n и k. Мы должны определить параллельные прямые к этим прямым.

Для начала, давайте определим, что такое параллельные прямые. Две прямые называются параллельными, если они никогда не пересекаются и не расположены на одной прямой.

Заметим, что прямые m и n пересекают секущую р, но никогда не пересекаются друг с другом. Это значит, что прямые m и n не могут быть параллельными.

Прямая k также пересекает секущую р, но не пересекает прямые m и n. Мы можем видеть, что прямые m, n и k расположены на одной стороне от секущей р. Это означает, что прямая k параллельна прямым m и n.

Обоснование:
Для того чтобы доказать, что прямая k параллельна прямым m и n, мы можем использовать определение параллельных прямых и свойства углов, образованных пересекающимися прямыми и секущими.

Если две прямые пересекаются секущей и образуют соответственные одноименные углы, то эти прямые параллельны друг другу. В данном случае, углы A и D, а также углы B и E являются соответственными одноименными углами. Поэтому, мы можем заключить, что прямые m и k параллельны, так как у них соответственные одноименные углы A и D. Аналогично, углы C и F указывают на параллельность прямых n и k.

Таким образом, параллельными прямыми к прямым m и n будут прямые, которые проходят через точки A и D, а также прямые, которые проходят через точки C и F.