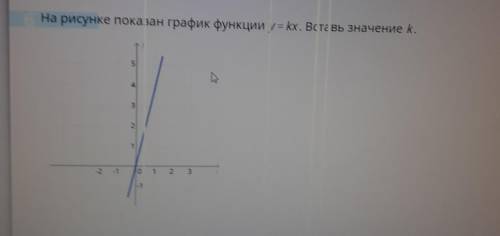
На рисунке показан график функций y=kx вставь значение k
Другие вопросы по теме Алгебра
Популярные вопросы
- I. Установите соответствие между видами гаметогенеза и особенностью половых...
2 - Як підкреслювати стоїть замислившись стара груша в саду !...
2 - Мәтіннен күрделі сөздерді теріп жаз, Құқық нормасы —бұл адамдардың белгілі...
2 - 2 cos(pi*x-pi)=корень из решить...
1 - Используя схему, расскажите, какие неорганические вещества входят в эко-систему....
2 - Если рамку с током поместить в магнитное поле вдоль его линий, то... Среди...
2 - На рисунку зображено схему ділянки електричного кола. Кожний резистор має...
2 - Людина рівномірно піднімає відро з водою на висоту 20 м за 20 с. Яку потужність...
1 - сделать таблицу по географии 9 класс. Хозяйство Северного Кавказа. Особенно...
1 - Как вы поняли, ЧТО великое, мощное и святое жило и горело в чудесном докторе?...
2
В функции y=kx число k называется угловым коэффициентом.
Он равен тангенсу угла между прямой и положительным направлением оси абсцисс.
Опустим из точки (1; 4) отрезок, параллельный оси ординат, чтобы получился прямоугольный треугольник.
Угловой коэффициент прямой будет равен тангенсу угла α.
Тангенс острого угла прямоугольного треугольника — это отношение противолежащего катета к прилежащему.
k = tgα = 4 : 1 = 4.
ответ: k = 4.
Давайте выберем две точки, которые лежат на прямой. На графике отмечены две такие точки: (2, 4) и (-3, -6).
Используя координаты этих точек, мы можем вычислить значение коэффициента наклона k. Формула для нахождения коэффициента наклона выглядит следующим образом:
k = (y2 - y1) / (x2 - x1)
Где:
y1 и y2 - значения по оси y для первой и второй точки соответственно;
x1 и x2 - значения по оси x для первой и второй точки соответственно.
Применим эту формулу для наших выбранных точек:
k = (-6 - 4) / (-3 - 2)
k = -10 / -5
k = 2
Таким образом, значение k равно 2. Ответ на задачу - k = 2.