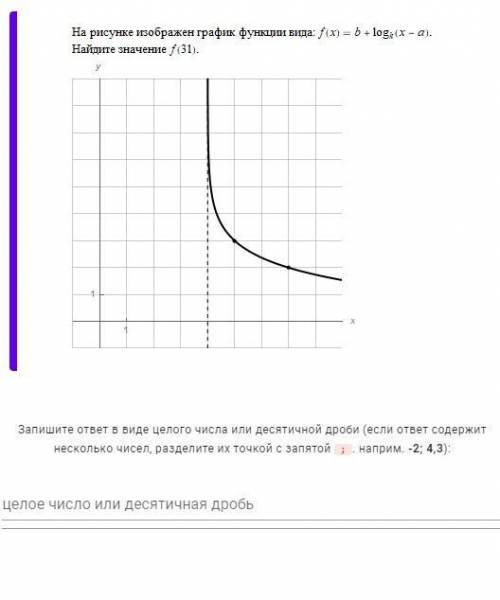
На рисунке изображен график функции вида f(x) = b +logk(x-a) Найдите значение f(31)
точки (5;3) (7;2)
Другие вопросы по теме Алгебра
Популярные вопросы
- Используя правило умножения в столбик и свойства умножения, вычислите: а) 1547·...
1 - Реши уравнение 132482-(х-28294)=114248...
2 - Яку синтаксичну роль може виконувати дієприкметник?...
1 - Письменный рассказ о любом персонаже в сказке о мёртвой царевне и о семи богатырях...
2 - Учащихся поехали на экскурсию в двух автобусах в одном автобусе было 25 человек...
2 - Решить! меньшее основание равнобедренной трапеции равно 5 см/ высота проведенная...
3 - Цены билета для проезда в купейном вагоне на 100% выше, чем цена в плацкартном...
3 - Степень с рациональным показателем. вычислите 1) 64 ^1/2 + 27 ^1/3 - 8 ^2/3 2)...
1 - Іть, будь ласка, скласти речення за схемою. схема така- ,,п? - а....
3 - Определите, когда по московскому времени должен совершить посадку самолет в воронеже,...
2
На рисунке даны две точки (5;3) и (7;2). Используя эти точки, мы можем найти значения для b, k и a.
1. Найдем значение для b:
Из первой точки (5;3) мы можем заменить x = 5 и f(x) = 3 в уравнение функции:
3 = b + logk(5-a)
2. Найдем значение для k:
Из второй точки (7;2) мы можем заменить x = 7 и f(x) = 2 в уравнение функции:
2 = b + logk(7-a)
У нас есть два уравнения с двумя неизвестными (b и a). Мы можем решить эту систему уравнений, используя метод подстановки или метод исключения.
Давайте вначале решим первое уравнение относительно b:
3 = b + logk(5-a)
b = 3 - logk(5-a)
Теперь подставим это второе уравнение вместо b:
2 = (3 - logk(5-a)) + logk(7-a)
Решаем это уравнение и находим значение для a:
2 = 3 - logk(5-a) + logk(7-a)
-1 = - logk(5-a) + logk(7-a)
logk(7-a) - logk(5-a) = 1
Теперь мы можем объединить логарифмы с правой стороны уравнения, используя свойство логарифма:
logk((7-a)/(5-a)) = 1
Теперь избавимся от логарифма, возведя обе части уравнения в степень k:
(7-a)/(5-a) = k^1
(7-a)/(5-a) = k
Когда k равно (7-a)/(5-a), мы получаем значение для k.
Теперь, имея значения для b, k и a, мы можем подставить x = 31 в уравнение функции, чтобы найти значение f(31):
f(31) = b + logk(31-a)
В результате у нас будет окончательный ответ, значение f(31) на графике функции f(x) = b + logk(x-a).