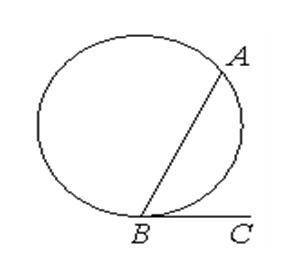
На окружности отмечены точки A и B так, что меньшая дуга AB равна 84°. Прямая BC касается окружности в точке B так,
что угол ABC острый. Найдите угол ABC. ответ
дайте в градусах.
Другие вопросы по теме Алгебра
Популярные вопросы
- Прочитай. Соедини линией рисунок с тем видом речи, к которому он может быть...
3 - Рассмотри рисунок. Составь по рисунку диалог. Разыграй с товарищем по парте...
1 - Рассмотри рисунки. Подбери к ним общее название и запиши его. рё зо но бо...
3 - Прочитай коту и собачке собрать скороговорки из слогов. Выучи любую скороговорку....
1 - Прочитай. Впиши пропущенные буквы. • Проверь по учебнику (упр. 1, с. 52),...
2 - Напиши слова-названия рисунков в алфавитном порядке. • Проверь правописание...
3 - Рассмотри рисунки. Прочитай. насекомые муха жук • Напиши под рисунками названия...
3 - Прочитай стихи-загадки Г. Виеру о буквах. Соотнеси рисунки и загадки. Назови...
3 - Прочитай. Составь и запиши ответ на вопрос. где живет кит...
2 - Рассмотри рисунки и звуковые обозначения слов. [кон ] [к ит] [кот] [т игр]...
1
1. Из свойства окружности, угол, соответствующий данной дуге AB, будет равен половине этой дуги, то есть 84°/2 = 42°.
2. Также, из свойства касательных, угол между касательной и радиусом (проведенным в точке касания) всегда равен 90°. Таким образом, угол CBA равен 90°.
3. Углы треугольника всегда в сумме равны 180°. Таким образом, угол ABC можно найти, вычтя уже известные углы (42° и 90°) из 180°:
ABC = 180° - 42° - 90°
Теперь можно решить эту задачу с помощью калькулятора:
ABC = 180° - 42° - 90°
ABC = 48°
Ответ: угол ABC равен 48°.