1. Алгебра
  2. На обработку одной детали первый

На обработку одной детали первый рабочий затрачивает на 1 мин меньше, чем второй рабочий. сколько деталей обрабатывает первый рабочий за 20 мин, если известно, что он обрабатывает за это время на 1 деталь больше, чем второй рабочий?

saule19611225 saule19611225    2   20.05.2019 21:40    0

Ответы
Ekaeterina44 Ekaeterina44  14.06.2020 11:59

Пусть второй рабочий обрабатывает деталь за t минут, а скорость обрабатывания детали x - деталей в минуту. Уравнение xt=1.

 

Тогда первый рабочий обрабатывает деталь за (t-1) минут, а скорость обрабатывания детали  y - деталей в минуту. Уравнение y(t-1)=1.

 

Первый рабочий обработает за 20 минут (20у) деталей. Второй рабочий обработает (20х) деталей. Известно, что первый обрабатывает а одну больше. Уравнение 20у=20х+1.

 

Составляем систему из 3-х уравнений и 3-х неизвестных.

\begin{cases} xt=1\\y(t-1)=1\\20y=20x+1 \end{cases}

 

Выражаем t из первого уравнения и подставляем во второе.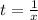 t=\frac{1}{x}

\begin{cases} y(\frac{1}{x}-1)=1\\20y=20x+1 \end{cases}

 

Упрощаем

\begin{cases} \frac{y}{x}-y=1\\20y=20x+1 \end{cases}

\begin{cases} y-yx=x\\20y=20x+1 \end{cases}

 

Из второго уравнения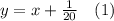 y=x+\frac{1}{20}\quad(1)

 

Подставляем в первое уравнение

x+\frac{1}{20}-\left(x+\frac{1}{20}\right)*x=x

Сокращаем обе части на слагаемое х.

\frac{1}{20}-\left(x+\frac{1}{20}\right)*x=0

 

Умножаем обе части на 20.

1-\left(20x+1\right)*x=0

1-20*x^2-x=0

20x^2+x-1=0

D=1+4*20

D=81

D=9^2

x_{1,2}=\frac{-1\pm\sqrt{D}}{2*20}

x_{1,2}=\frac{-1\pm9}{2*20}

Отрицательный ответ не подходит по смыслу задачи. Скорость не может быть отрицательной.

x=\frac{-1+9}{2*20}

x=\frac{8}{2*20}

x=\frac{1}{5}

 

Подставляем х в (1).

 

y=\frac{1}{5}+\frac{1}{20}

y=\frac{4}{20}+\frac{1}{20}

y=\frac{5}{20}

y=\frac{1}{4}

За 20 минут первый рабочий обработает 20*у деталей. То есть 20/4=5 деталей.

 

ответ:  за 20 минут первый рабочий обработает 5 деталей.

 

P.S. можно было и полегче, только я не задумывалась об этом.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
nastiamakeeva0 nastiamakeeva0  30.09.2019 04:00
Бабушка копала 1/3 огорода 8 часов, дед копал 1/3 огорода 12 часов сколько они будут копать оставшуюся 1/3 вместе? ответ 288 мин...
rfrfirb2016oy0uz3 rfrfirb2016oy0uz3  13.05.2021 14:01
По братски решите ответ с решением это контрольная умоляю просто...
Ionely Ionely  13.05.2021 14:00
Вкладник поклав до банку 5 000 грн. під 16% річних. а) Яким буде вклад через 2 роки?б) Скільки відсоткових грошей матиме вкладник через2 роки?​...
18alinochka150 18alinochka150  13.05.2021 14:00
Разложить на множители 27+b⁹​...
Mabmbj Mabmbj  13.05.2021 14:00
Решите систему уравнений ГРАФИЧЕСКИМ . y-x^2=0y-2x=0 ​...
няшка366 няшка366  13.05.2021 13:59
Знайдіть суму шістнадцяти перших членіварифметичної прогресії (а), якщо a = 1,a = 2,8​...
Мейси13 Мейси13  13.05.2021 13:59
Постройте график функции у = - (х – 3) (х +2) и укажите его наибольшее значение и промежуток возрастания. ​...
про100Banan про100Banan  09.03.2019 22:40
6/(x^2-36)+1/(36-12x+x^2)+1/(2x+12)=0...
sirentuhfatull sirentuhfatull  09.03.2019 22:40
Доследить функцию на экстремум у=3-х3...
csonzdanova csonzdanova  09.03.2019 22:40
Два автобуса одновременно отправляются с одной площади по маршрутам(разным). у одного рейс туда и обратно - 48 минут, у другого 1,12 минут. через сколько времени автобусы...

Популярные вопросы