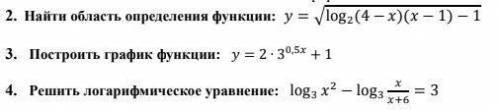
Алгебра: Можно решить с объяснением .

Можно решить с объяснением .

Ответы

Эллада20029 29.07.2021 00:29

2) D(y)=(-∞; -6]∪[1; +∞)

3)Смотреть изображение

4)-9; 3

Объяснение:

2) Область определения ф-ции - все значения, которые может принимать независимая переменная (х). Подкоренное выражение корня чётной степени должно быть не меньше нуля, поэтому чтобы найти область определения нужно решить неравенство

$log_2(4-x)(x-1)-1\geq 0\\log_2(4-x)(x-1)\geq 1\\(4-x)(x-1)\geq 2\\4x-4+x^2+x-2\geq 0\\x^2+5x-6\geq 0\\D=25+24=7^2\\x_1=-6\\x_2=1\\(x+6)(x-1)\geq 0$

x∈(-∞; -6]∪[1; +∞)

Тогда D(y)=(-∞; -6]∪[1; +∞)

3) Чтобы построить график функции нужно построить график обычной показательной функции без второстепенных коэффициентов. Берём любые значения икса и считаем чему при данных значениях будет равен игрек. Точки с полученными координатами выставляем на координатную плоскость и проводим через эти точки график функции. Потом смещаем график в соответствии с коэффициентами. Свободные коэффициенты указывают на сколько клеток нужно сместить график по ординате. Коэффициент перед иксом Сжимает график по абсциссе обратить внимание, что данная функция является показательной и абсцисса здесь будет являться асимптотой, и график её никогда не пересечёт, хотя будет всё больше и больше приближаться к ней.

$log_3x^2-log_3\frac{x}{x+6} =3\\log_3\frac{x^2(x+6)}{x} =3\\\frac{x^2(x+6)}{x} =27\\x^3+6x^2-27x=0\\\\x(x^2+6x-27)=0\\x_1=0\\x^2+6x-27=0\\D=36+108=12^2\\x_2=-9\\x_3=3$