1. Алгебра
  2. Можно ли решить это с формул

Можно ли решить это с формул комбинаторики? у меня получилось только первый пункт решить

VaneK12354 VaneK12354    2   01.08.2019 12:31    0

Ответы
nargis84002 nargis84002  03.10.2020 19:38

Общее число возможных элементарных исходов равно числу которыми можно извлечь 3 шара из 8:

C^3_{8}=\dfrac{8!}{3!5!}=56

Количество благоприятных исходов:

а) Подсчитаем сколькими можно вынуть 3 красных шара.

это можно сделать C^3_{4}=4

Вероятность того, что все 3 шарика красные, равна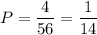 P=\dfrac{4}{56}=\dfrac{1}{14}

б) Подсчитаем сколькими можно вынуть 2 шарика красного цвета и 1 желтого. Красных 2 шарика можно выбрать C^2_4=\dfrac{4}{2!2!}=6 а 1 желтого По правилу произведения, таких

Вероятность того, что среди выбранных 3 шаров будет 2 красного цвета и 1 желтого, равна P=\dfrac{24}{56}=\dfrac{3}{7}

в) Подсчитаем сколькими можно выбрать 3 шарика одного цвета. Три красных шара мы посчитали в пункте а таких 4, аналогично, выбрать три желтых шара можно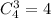 C^3_4=4 По правилу сложения, таких

Вероятность того, что среди трех выбранных шаров будет все шарики одного цвета, равна P=\dfrac{8}{56}=\dfrac{1}{7}

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
арбуз30 арбуз30  20.09.2021 18:33
-2×-4,5+5×2,2ЗА ПОДРОБНОЕ РЕШЕНИЕ ПОДПИШУСЬ...
755766 755766  20.09.2021 18:35
Дана функция y=f(x), где f(x)=8,2x. Решить: f(sin2x)⋅f(cos2x)....
trinadsyear trinadsyear  20.09.2021 18:38
Пример на картинке (обезательно нужен ответ чтобы подходил под нужное окно которое на скрине)...
vladyulin vladyulin  20.09.2021 18:41
решить. Буду благодарен! Задание в фото. ⬇️...
windi37 windi37  20.09.2021 18:42
емае Прочитай выражение и найди его значение.В данном числовом выражении 4,6−2,1 данаПрочитай выражение и найди его значение.В данном числовом выражении 4,6−2,1 дана -...
rustikkhusnutdi rustikkhusnutdi  20.09.2021 18:47
Запишите числа в виде периодической десятичной дроби...
вика8914 вика8914  20.09.2021 18:51
решить За три дня турист 64км причём в первый день он 3/8 всего пути,а во второй день 50% оставшегося пути. Сколько турист в третий день...
3458 3458  13.07.2019 17:00
Как решить лимит lim x- к бесконечности (2n+5/2n+7)^2n+1...
maksCRAFTer maksCRAFTer  13.07.2019 17:00
Запишите степень , которая получится если выражение с6 возвести в третью степень...
denissneganatan denissneganatan  13.07.2019 17:00
Найдите два целых числа,между которыми находится 48 под корнем...

Популярные вопросы