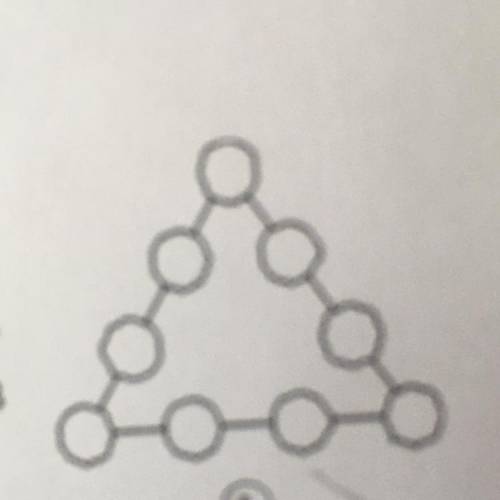
Можно ли расставить в кружочки натуральные числа от 1 до 9 так, чтобы сумма чисел по всем сторонам треугольника была одной и той же, а сумма чисел в вершинах равнялась 9? Привести пример, если да. Доказать почему, если нет
Другие вопросы по теме Алгебра
Популярные вопросы
- Почему 10-20-е гг. хix в. стали временем подьема революционного движения в различных...
3 - Двое соседей-дачников собрались построить мост через ручей, разделяющий их дачные...
1 - Что сделал бартоломеу диаш в 1487-1488гг. (кратко)...
3 - Азербайджанский стайер хайле ибрагимов установил в 2011 году новый рекорд азербайджана,пробежав...
2 - Какие новые герои появились в 17 века...
3 - Какие кустарники первыми сбрасывают листья,а какие последними?...
1 - Нужно ответить на вопросы по тексту текст: my name is alexander alex or short....
1 - Округлите число 4 839 615 до десятых; до сотен; до тысяч; до десятков тысяч; до...
2 - Ввражение 0.4*(3m+0.7a)-5*(0.3m-0.4a)...
1 - Вуголовном кодексе рф нет следующего состава преступления: 1)присвоение или растрата...
1
Нет
Объяснение:
Сумма цифр от 1 до 9 равна 45. Если считать сумму трёх сторон, то можно заметить, что числа в вершинах считаются два раза, то есть сумма по всем сторонам равна 45 + 9 = 54. Сумма одной стороны, следовательно, равна 54 / 3 = 18.
Заметим, что цифра 9 не может стоять в вершине, иначе оставшиеся цифры в вершинах равны нулю, что невозможно. Тогда она стоит между цифрами в вершинах (пусть эти цифры равны a и b, а цифра в третьей вершине — c). Пусть оставшееся число на этой стороне равно x. Тогда 9 + a + b + x = 18 ⇒ x = 9 - (a + b). Но так как a + b + c = 9, c = 9 - (a + b). То есть x = c, что невозможно, поскольку все цифры разные. Противоречие.