Может ли быть равным числу 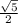$\frac{ \sqrt{5} }{2}$
значение:
а) sin a

б) cos a

в) tg a

г) ctg a

написать ответы с решением (пояснением), т.к. правильный ответ уже имеется.

Ответы

ymniy4 24.01.2024 17:56

Для того чтобы решить это уравнение, нам необходимо знать значения тригонометрических функций на различных углах.

Чтобы ответить на этот вопрос, нам нужно знать значение функций синус, косинус, тангенс и котангенс для угла а.

По определению, sin a = противолежащий катет / гипотенуза и cos a = прилежащий катет / гипотенуза.

tg a = sin a / cos a и ctg a = cos a / sin a.

Из данного вопроса известно, что значение равно $\frac{ \sqrt{5} }{2}$ .

Для того чтобы найти значение конкретной функции, мы можем использовать значения известных тригонометрических отношений.

а) sin a:
Так как sin a = противолежащий катет / гипотенуза,
мы можем найти значение sin a, используя известный множитель $\frac{ \sqrt{5} }{2}$ .

Рассмотрим прямоугольный треугольник, где противолежащий катет равен $\frac{ \sqrt{5} }{2}$ и гипотенуза равна 1.
Тогда мы можем найти прилежащий катет, используя теорему Пифагора:

противолежащий катет^2 + прилежащий катет^2 = гипотенуза^2.

( $\frac{ \sqrt{5} }{2}$ )^2 + прилежащий катет^2 = 1^2.

(5/4) + прилежащий катет^2 = 1.

прилежащий катет^2 = 1 - (5/4) = 4/4 - 5/4 = -1/4.

Так как прилежащий катет является длиной, он не может быть отрицательным.
Это означает, что sin a не может быть равным $\frac{ \sqrt{5} }{2}$ .

Ответ на вопрос а) равен "нет".

б) cos a:
Аналогично, используя противолежащий катет и гипотенузу известной дроби $\frac{ \sqrt{5} }{2}$ ,
мы можем использовать теорему Пифагора, чтобы найти прилежащий катет:

противолежащий катет^2 + прилежащий катет^2 = гипотенуза^2.

(5/4) + прилежащий катет^2 = 1^2.

прилежащий катет^2 = 1 - (5/4) = 4/4 - 5/4 = -1/4.

Подобно ответу а), прилежащий катет не может быть отрицательным.
Это означает, что cos a тоже не может быть равным $\frac{ \sqrt{5} }{2}$ .

Ответ на вопрос б) также равен "нет".

в) tg a:
tg a = sin a / cos a.
Так как мы уже установили, что sin a и cos a не могут быть равными $\frac{ \sqrt{5} }{2}$ ,
это означает, что tg a также не может быть равным $\frac{ \sqrt{5} }{2}$ .

Ответ на вопрос в) равен "нет".

г) ctg a:
ctg a = cos a / sin a.
Так как мы уже установили, что sin a и cos a не могут быть равными $\frac{ \sqrt{5} }{2}$ ,
это означает, что ctg a также не может быть равным $\frac{ \sqrt{5} }{2}$ .

Ответ на вопрос г) также равен "нет".

Итак, ответ на данный вопрос для всех значений функций равен "нет".
Ни одна из указанных тригонометрических функций не может быть равной $\frac{ \sqrt{5} }{2}$ .

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра