1. Алгебра
  2. Моторная лодка км против

Моторная лодка км против течения, 32 км по течению, затратив на весь путь 3 часа. найти собственную скорость лодки, если скорость течения реки 1 км/ч

maksimiksanov maksimiksanov    3   26.07.2019 14:10    0

Ответы
gyulmalievasab gyulmalievasab  24.09.2020 22:56

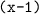Пусть собственная скорость равна \texttt{x} км/ч, тогда скорость против течения равна \texttt{(x-1)} км/ч, а по течению - 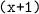\texttt{(x+1)} км/ч. Время, затраченное лодкой против течения равно 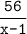\displaystyle\frac{\texttt{56}}{\texttt{x-1}} ч, а по течению - 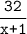\displaystyle\frac{\texttt{32}}{\texttt{x+1}} ч. На весь путь лодка затратила 3 часа.


Составим и решим уравнение

\displaystyle\frac{\texttt{56}}{\texttt{x-1}} +\displaystyle\frac{\texttt{32}}{\texttt{x+1}} =\texttt{3}~~~|\cdot\texttt{(x-1)(x+1)}\\ \\ \texttt{56(x+1)+32(x-1)=3(x-1)(x+1)}\\ \\

\displaystyle 56x+56+32x-32=3x^2-3


{3x^2-88x-27}={0}

D=b^2-4ac=(-88)^2-4\cdot3\cdot(-27)=8068

x_1=\dfrac{88+2\sqrt{2017}}{6} \approx30 км/ч.

x_2=\dfrac{88-2\sqrt{2017}}{6} - посторонний корень

ответ: 30 км/ч.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
gorodo gorodo  12.05.2021 19:32
АЛГЕБРА. 7 КЛАС! Зробіть все що можете, завтра здавати...
AlecsandrPonkratov77 AlecsandrPonkratov77  12.05.2021 19:32
Нужна , буду очень благодарен​...
Fissadi Fissadi  12.05.2021 19:33
какие из чисел а) 1; б) 0; в) 2; г) -5; д) 1.5; е) -2/3 является корнем уравнения (x-1)*(x+5)*(3x+2)*(2x+3)*(x+1,3) = 0​...
ivanovali0109 ivanovali0109  12.05.2021 19:33
Решите системы ) В) 8у — 52 = 23,Зу – 22 = 6;Д) 7x+4y=743x+2y=32E)11u+15v=1,9- 3u+5v=1,3​...
aselduishenova aselduishenova  12.05.2021 19:33
Контрольная работа по алгебре 7 класс макарычев...
Lizaveta9999 Lizaveta9999  18.02.2022 21:37
оберіть послідовність чисел яка є арефметичною послідовністю 5;0;5;0 13;13;13;13 2;7;12;17 2;-2;-8;-12...
makssabarov makssabarov  18.02.2022 21:44
Знайдіть значення аргументу, при якому при якому значення функції y=-3x+4 дорівнює 16...
DamirJonson DamirJonson  18.02.2022 21:45
Каждую систему решить тремя : графически, подстановкой, сложением...
yaantonio19 yaantonio19  18.02.2022 21:54
Внесите множитель под знак корня: 1. 5√2=√25•√2= 2. 0,5 √30= 3. -7 √10=-√49•√10= 4. -4 √2= 5. 3 √2/3= 6. 2 √3,5m= 7. 6 √а/12= 8. 2/9 √243c=...
gabjagYT gabjagYT  14.07.2019 23:50
Найдите корни уравнения: 1)12x^2-28x-2=3? ?...

Популярные вопросы