Монета подброшена 120 раз. Найти вероятность следующих событий: а) гербов выпало ровно 60 раз; б) герб выпал не меньше 50 или больше 70 раз

Ответы

natalimironenko 17.08.2020 19:21

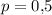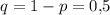Всего n = 120 испытаний. Вероятность успеха в одном испытании p=0{,}5 , соответственно вероятность противоположного события q=1-p=0{,}5 .

а) Для больших n будем использовать локальную теорему Лапласа

$x=\dfrac{k-np}{\sqrt{npq}}=\dfrac{60-120\cdot 0{,}5}{\sqrt{120\cdot 0{,}5\cdot 0{,}5}}=0$

Искомая вероятность: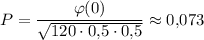 $P=\dfrac{\varphi(0)}{\sqrt{120\cdot 0{,}5\cdot 0{,}5}}\approx 0{,}073$

где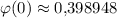 $\varphi(0)\approx 0{,}398948$ .

б) Применяем форму интегральной теоремы Лапласа

$x_1=\dfrac{k_1-np}{\sqrt{npq}}=\dfrac{50-120\cdot 0{,}5}{\sqrt{120\cdot 0{,}5\cdot 0{,}5}}\approx -1{,}83;\\ \\ x_2=\dfrac{k_2-np}{\sqrt{npq}}=\dfrac{70-120\cdot 0{,}5}{\sqrt{120\cdot 0{,}5\cdot 0{,}5}}\approx 1{,}83$

Искомая вероятность:

$P_{120}\Big(50$

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра

даниил853 26.05.2019 05:20

Два числа называются симметричными если порядок цифр в одном из них слева направо совпадает с порядком цифр другого числа справа налево. чему равна разность двух симметричных...

rus7300 26.05.2019 05:20

Найти число зная что 2/5 части от 3/4 этого неизвестного составляют 24...

хотам3 26.05.2019 05:20

Усамой ..у самой не получается( известно,что ctg(t-п)=-3/4 и п/2...

MASTER10011 26.05.2019 05:20

Аво второй степени в минус ав плюс а во второй степени с минус ас...

fatimatangatar 26.05.2019 05:20

Постройте график функции y=3sin(x-п/6)...

smoke228322 26.05.2019 05:20

Что можно сказать про выпуклость и вогнутость...

irinatalanina95 26.05.2019 05:20

Укажите трехчлен который принимает только положительные значения х(во второй степени)+8х+16 3х(во второй степени)-10х+9 12х-х(во второй степени)-34 8х-х(во второй степени)-18...

mqu 27.12.2020 13:50

Решите уравнение графическим...

bigarnastia 27.12.2020 13:50

Замените х степенью с основанием так, чтобы полученное равенство было тождеством: а) с²х=с⁵б) хс⁵=с⁹в) с⁶х=с¹¹г) с⁴х=с¹⁵...

smchnc2004 27.12.2020 13:51

Знайдіть значення многочлена x^3+5xy якщо x=3, y=-2...

Монета подброшена 120 раз. Найти вероятность следующих событий: а) гербов выпало ровно 60 раз; б) герб выпал не меньше 50 или больше 70 раз

Популярные вопросы