Многочлен с целыми коэффициентами
называется хорошим если наибольшим общий делитель его коэффициентов равен
1) докажите что произведение двух хороших многочленов снова является хорошим много членом
Другие вопросы по теме Алгебра
Популярные вопросы
- Политика Филиппа 1политика Франциска 1...
3 - Найдите величину по ее дроби: 1) 4/7 ее равны 16 м; 2)5/8 ее...
2 - Келешектің мамандықтарыДиалогтітында. Сұрақтар мен жауаптарды...
2 - Чи завжди продукти екскреції є непотрібними відходами метаболізму...
1 - начинающему исследователю» составьте схему процесса превращения...
1 - Қазақстан тарихы *Шілікті және бесшатыр патша қорғандары 2-са...
2 - Оберіть правильну відповідь ! До ть!!) . Приголосні д, т, з,...
3 - 3) 2х+9 =-6-5х 4) -7х+6 = х-8 5) 4+5х = -2-х 6) 5-2х = х+11 7)...
3 - подскажите с ответом и решением ...
1 - стих короткий для 5 класса...
1
Пусть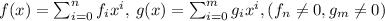 - хорошие.
- хорошие.
Пусть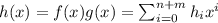 не хороший. Тогда, по определению, существует такое простое число
не хороший. Тогда, по определению, существует такое простое число 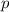 , которое нацело делит все
, которое нацело делит все 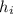 . По определению
. По определению 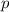 не может делить все
не может делить все 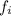 и
и 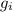 .
.
Пусть минимальные по номеру коэффициенты многочленов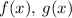 , не делящиеся на
, не делящиеся на 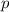 , равны
, равны 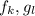 .
.
Тогда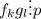 . Т.к.
. Т.к. 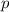 - простое, то хотя бы один из
- простое, то хотя бы один из 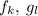 кратен
кратен 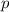 .
.
Противоречие с тем, что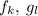 не делятся на
не делятся на 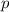 .
.
А значит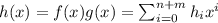 хороший.
хороший.