много !
связанно с функциями!
все 4 ! тесты!

1) Д

2) А

3) Б

4) Б

Объяснение:

Свойства и определения:

Функция четная, когда

f(x) = f(-x)

и нечетна, когда

f(x) = -f(x)

3) у = х^4 + х^2 + 1

у(-х) = (-х)^4 + (-х)^2 + 1 =

= х^4 + х^2 +1 = y(x)

так как (-х)^2n = x^2n для любого целого n

4) y = 1 / (x^3 - x)

y(-x) = 1 / [(-x)^3 - (-x)] =

= 1 / (-x^3 + x) =

= -1 / (x^3 -x) = -y(x)

так как (-х)^(2n+1) = -x^(2n+1) для любого целого n

1)  График любой чётной функции симметричен относительно оси ОУ. То есть, если перегнуть график по оси ОУ, то линия в правой полуплоскости совпадёт с линией в левой полуплоскости. Таким свойством обладает график Д).

2)  График любой нечётной функции симметричен относительно точки О(0,0), начала координат. Это график А).

3)  Чётная функция обладает свойством: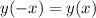    . Такой функцией является функция  Б), так как

4)  Нечётная  функция обладает свойством: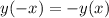    . Такой функцией является функция  Б), так как