мне введения новой переменной решите уравнения (только 2 уравнение)!
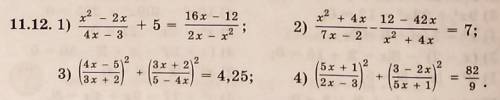
Другие вопросы по теме Алгебра
Популярные вопросы
- Какой из перечисленных народов не проживает на территории италии 1) славяне...
1 - :назови причину болезни хоттабыча и как его...
2 - Қр ұға,ұбт,ақш,бұұ,қхр,тмдт,тжо,аақ толық сөздер...
3 - Что вы узнали о жизни сына дубровского( дубровский)...
3 - 1\4 от 16 1\3 от 18 1\2 от 16 1\12 от 12...
3 - Найди значение одночлена (1)-степень 1)3n(3) если n=-2 2)-4.5xy(2) если х= 1/9...
1 - Разберите по составу слова негромко, окруженной ,реченка....
3 - Авсd - трапеция,через с провели прямую параллельную ав до аd ( в т.e ) de=6...
2 - Составить три предложения и выписать все словосочетания...
1 - 1.образование листьями хлорофила на свету? 2.обнаружение дыхания листьев? 3.обнаружение...
3
Объяснение:
ОДЗ:
Введём замену:
Перепишем уравнение с учётом замены:
Вернёмся к замене:
Корни удовлетворяют ОДЗ.