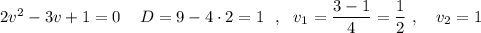мне нужно полное решение и ответ

Другие вопросы по теме Алгебра
Популярные вопросы
- Complete the sentences. 1) If you add a of salt, it’ll be better. 2)...
1 - Кусок полатна в 124м надо разделить на 2 части так, что длина одной части...
3 - 1-тапсырма Кейіпкердің әрекеттері мен портретін образды ашуда қолданыңызАвтордың...
2 - 1) На координатной прямой отмечены точки?...
1 - с написанием сочинения А.А.Пластов. Первый снег...
3 - Ұлы адамдар достығы 3-тапсырма Дербез пікір жазу тәсілін қолданып,өлеңдердің...
1 - Можно ли воздействовать без слов?...
1 - B 6420 Rand the adidexcerpt from Oliver Thot,novel about a poor orphagrowing...
1 - Чтобы построить график линейной функции достаточно взять Укажите правильный...
3 - написать сочинение по этой картине...
3
Введём замену: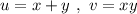
Решим квадратное уравнение