1. Алгебра
  2. Между какими соседними

Между какими соседними целыми числами заключено значение выражения: 1/(√3 +1)+1/(√5+√3)+1/(√7+√5)+…+1/(√21+√19)

ssqllxx ssqllxx    1   15.03.2019 14:10    3

Ответы
margaritavladim margaritavladim  25.05.2020 13:00

избавляясь от ирациональность (используя формулу разности квадратов, сводя все у общему знаменателю и уничтожая одинаковые слагаемые по значению, но разные по знаку), получим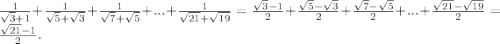\frac{1}{\sqrt{3} +1}+\frac{1}{\sqrt{5}+\sqrt{3}}+\frac{1}{\sqrt{7}+\sqrt{5}}+...+\frac{1}{\sqrt{21}+\sqrt{19}}= \frac{\sqrt{3} -1}{2}+\frac{\sqrt{5}-\sqrt{3}}{2}+\frac{\sqrt{7}-\sqrt{5}}{2}+...+\frac{\sqrt{21}-\sqrt{19}}{2}= \frac{\sqrt{21}-1}{2}.

 

4<\sqrt{21}<5;</p&#10;<p4-1<\sqrt{21}-1<5-1;</p&#10;<p3<\sqrt{21}-1<4</p&#10;<p1<\frac{3}{2}<\frac {sqrt{21}-1}{2}<\frac {4}{2}=2

ответ: между 1 и 2

 

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
kateadel01 kateadel01  13.05.2020 22:52
На рисунке изображён график дифференцируемой функции y=f(x). На оси абсцисс отмечены семь точек: x1, x2, ...,х7 В скольких из этих точек производная функции y=f(x)...
sofija97 sofija97  13.05.2020 22:52
Завтра надо сдать, а я не понимаю тему с решением​...
228Aimer228 228Aimer228  13.05.2020 22:52
В магазин привезли для продажи 15 лодок импортного производства и 5 лодок отечественного производителя. Какова вероятность того, что первые две купленные лодки...
darya21072005 darya21072005  13.05.2020 22:52
Найдите промежутки возрастания и убывания функции, определите точки экстремума: 1. y=x^3-6x^2+9x+62 2. y=x^3+17,5x^2+50x+18 3. y=-19+108x+x^3 4. y=-9x^2-x^3+6 5....
Merlin131 Merlin131  14.08.2019 14:15
Решить, только с подробным решением по действиям. 1) y(x)=4x^2-5x+1 x=? 2) y(x)=3x^2+x-2 x=? 3) y(x)=x^2-2x-3 x=? 4) y(x)=3x^2-2x-5 x=?...
масяня194 масяня194  14.08.2019 14:01
Найдите наибольшее целое решение неравенства х⩽-5 . объясните если не сложно как нашли....
baskaqusar baskaqusar  14.08.2019 13:57
Во время сдачи зно автоматически получаешь сколько...
BatsonPlay BatsonPlay  14.08.2019 15:10
(4/9)х=(3/2)-5. показательные уравнение и неравенства...
Ibrolya Ibrolya  14.08.2019 13:50
Кто сможет решить эту графическим методом? найдите все такие значения параметра a , при каждом из которых наименьшее значения функции y=3|x+a|+|x^2-x-2| меньше...
vvndas1 vvndas1  14.08.2019 13:34
Решить 4 примера номер: 1.решите уравнения примеры под цифрами 1(а,б) и 2(а,б) буду...

Популярные вопросы