Мастер и ученик работая совместно могут выполнить за 6 ч 40мин.если сначала будет работать только мастер и выполнит половину , а затем его сменит

Question

Алгебра: Мастер и ученик работая совместно могут выполнить за 6 ч 40мин.если сначала будет работать только мастер и выполнит половину , а затем его сменит ученик и выполнит оставшуюся часть , то всего на выполнение будетизрасходовано 15 часов.за сколько часов могут выполнить мастер и ученик работая в отдельности? ?

agarkovr83 · Answer

Производительность мастера x, ученика - y. Вся работа - 1.

6 часов 40 минут это 6 целых 2/3 часа. Работая вместе они выполнят работу за 6 2/3, т.е.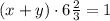 $\\(x+y)\cdot6\frac23=1$ . Половину работы мастер выполнит за 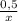$\frac{0,5}x$ часов, ученик за 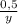$\frac{0,5}y$ часов, что в сумме даёт 15 часов, т.е.

$\\\frac{0,5}x+\frac{0,5}y=15$

Получаем систему из двух уравнений с двумя неизвестными:

$\\\begin{cases}(x+y)\cdot6\frac23=1\\\frac{0,5}x+\frac{0,5}y=15\end{cases}\Rightarrow\begin{cases}x=\frac3{20}-y\\200y^2-30y+1=0\end{cases}\\\begin{matrix}\begin{cases}x=\frac1{20}\\y=\frac1{10}\end{cases}&\quad&\begin{cases}x=-\frac1{20}\\y=\frac15\end{cases}\end{matrix}$

Второе решение не подходит, т.к. производительность не может быть отрицательной.

Следовательно, мастер может выполнить задание за 20 часов, ученик за 10 часов.

Популярные вопросы