Логарифмы! решить log2(x^2-6x+24)< 4 log6(14-4x)=log6(2x+2) решить хотябы 2
Ответы
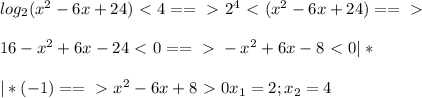
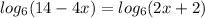 антиципируем, получаем простенькое уравнение
антиципируем, получаем простенькое уравнение 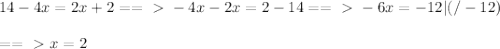
Другие вопросы по теме Алгебра
Популярные вопросы
- Построй квадрат со стороной 4 сантиметра найди его периметр разными...
1 - Arccos (-1/2) - arcsin корень 3/2 4 arctg 1 + 3 arctg (-1/корень3)...
2 - От данных глоголов в неопределенной форме образовать глаголы 3- его лица...
3 - Решить уровнение (одна цела 1/2-3/8}: 3...
1 - Написать сочинение про природу для 3его класса...
1 - 1. напишите реферат на тему «модернизация в россии в начале xviii века»....
1 - К200 г раствора с массовой долей 15% прибавил 100 грамм воды.массовая доля...
1 - Сторона основания и высота правильной треугольной пирамиды sabc равны 10...
2 - Сравните положение россии в мире в начале хх в. и в начале ххiв .в чем...
2 - Arccos (-1/2) - arcsin корень 3/2 4arctg 1 + 3arctg (-1/корень 3)...
1