Log0,5(x^2-1)*lg0,5<=0
Заранее ответившему❤️
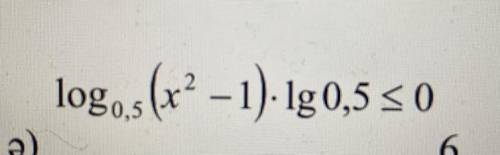
Другие вопросы по теме Алгебра
Популярные вопросы
- Что омывает Чёрное море в России?...
1 - При каком значении х значение выражения 17 умножить на x+6 умножить...
2 - Запиши решение неравенства надо...
2 - §13. Превращение США в мировую державу | 8 класс. Задание: Уберите...
1 - А4. В реанике ABC биссектриса ВК перпендикулярна стороне AC, AC = 18...
3 - Мне нужна написать характеристику из произведение Пинская шляхта В....
3 - Упростите вырожение 2-(x-1)(x^2+x+1)(x^3 +1), и найдите его значение...
2 - Какими частями речи могут быть выражены союзные слова? А) относительными...
1 - Міні-твір на тему цінності сучасної людини (за твором Божественна комедія...
1 - Напишите соченение по моей любимой рыбе по английскому (рыба любая)...
1
log(0.5) (x^2 - 1)*lg 0.5 <= 0
одз x^2 - 1 > 0
(x - 1)(x + 1) > 0
x ∈ (-∞, -1) U (1, +∞)
lg 0.5 = lg 5/10 = lg 5 - 1 < 0
log(0.5) (x^2 - 1) >= 0
log(0.5) (x^2 - 1) >= log(0.5) 1
Cнимем логарим и меняем знак неравенства, т к основание < 1
x^2 - 1 <= 1
x^2 - 2 <= 0
(x - √2)(x + √2) <= 0
x ∈ [-√2, √2]
учитываем одз x ∈ (-∞, -1) U (1, +∞)
ответ x ∈ [-√2, -1) U (1, √2]