1. Алгебра
  2. Log(1/2) |x| = |x| - 1

Log(1/2) |x| >= |x| - 1

Andrey26022002 Andrey26022002    2   16.02.2020 16:29    0

Ответы
SokolDev SokolDev  11.10.2020 05:36

\log_{0,5}|x| \geq |x| - 1

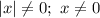
ОДЗ: |x| \neq 0; \ x \neq 0

Решим данное неравенство графически.

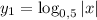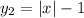Рассмотрим две функции y_{1} = \log_{0,5}|x| и y_{2} = |x| - 1 и изобразим их на координатной плоскости (см. вложение).

Из графика видно, что логарифмическая функция не меньше модульной на промежутке x \in [-1; \ 0) \cup (0; \ 1]

ответ: x \in [-1; \ 0) \cup (0; \ 1]


Log(1/2) |x| >= |x| - 1
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
diankaa55 diankaa55  02.12.2020 17:19
Добуток третього та шостого членів арифмітичної прогресії дорівнює 406. При діленні дев ятого члена на четвертий частка дорівнює 2 і остача 6. Знайти перший член і різницю...
nadiakrasavtze nadiakrasavtze  02.12.2020 17:20
Укажи абсциссу и ординату точки A(3;−3). ответ: абсцисса точки A ; ордината точки A ....
вика3662 вика3662  02.12.2020 17:21
Если одну сторону квадрата уменьшить на 2,4м, а вторую на 0,6м, то площадь полученного прямоугольника будет на 22,56 м2 меньше площади квадрата. Найди сторону квадрата....
panda7777777777 panda7777777777  02.12.2020 17:22
очень Постройте график функции f(x) = x^2 — 6х +8. Используя график, най дите :1)f(6): f(1):2) значения х, при которых f(x) = 8; f (x) = -1; f(x) = -2;3) наибольшее и наименьшее...
gspd000 gspd000  08.05.2020 10:40
Пользуясь свойствами тригонометрических функций расположите числа в порядке возрастания: sin0,5; sin7,6; sin4,1; sin(-0,9)....
amir158 amir158  08.05.2020 10:40
Параллельны ли прямые? Выберите правильный ответ из выпадающего списка. По рисунку установите параллельность прямых. 1 – 2 – 3 –...
GTmoonsoonall GTmoonsoonall  08.05.2020 10:40
При каком значении m значения выражений 3m, m^2+2, m+4 будут последовательными членами арифметической прогрессии? Найдите члены этой прогрессии. *с подробным объяснением...
001Карина11111 001Карина11111  08.05.2020 10:40
Функция задана формулой y=8x-3 оприделите проходит ли график функции через точку B(-2;-13)...
kotnapnewme123p04tz4 kotnapnewme123p04tz4  08.05.2020 10:40
Решите систему уравнений графическим пример на фото)...
таня1697 таня1697  08.05.2020 10:40
Найдите аргумент комплексного числа.1) z=5; 2) z=-2i; 3)z=√33дробь2-√11дробь2i....

Популярные вопросы