Lim xsin3x/tg²4x
x->0
решить предел, только НЕ по теореме Лопиталя
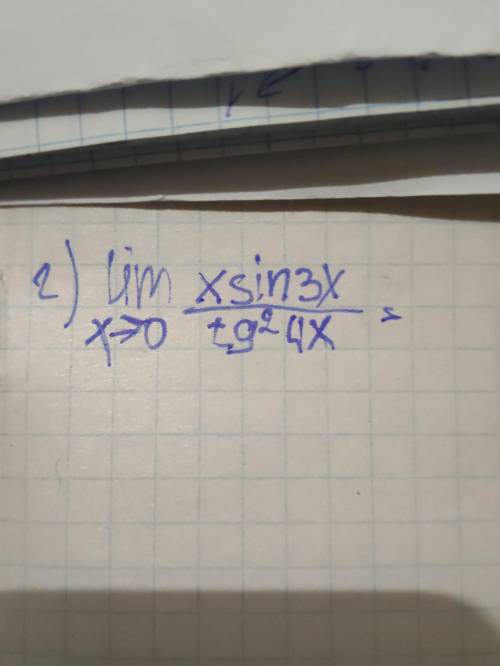
Другие вопросы по теме Алгебра
Популярные вопросы
- надо до завтра надо до завтра >...
3 - Знайди відношення 150 г до 1,5 кг...
2 - Здійсніть ланцюжок перетворень: (2, ) Ca →CaO → Ca(OH)2 → CaCO3 → CO2 → K2CO3...
2 - Задание выполняются в QBasic. Найти значение данной функции на отрезке [a,...
2 - 1 Запишите текст. Вставьте пропущенные буквы и объясните их написаниеграфически:(1)В...
1 - 3 3/23*(-11 4/9-(3.6):9/35)-4 5/6...
2 - Как автор знакомит читателя с Ивиными? Какие приёмы он использует при этом?...
1 - Який виграш в роботі дає важіль...
2 - Дан массив из n элементов. Необходимо найти количество элементов массива,...
2 - Как мне ответить есть мне сказали Саламалейкум ?...
1
ответ: 3/16
Объяснение:
Lim xsin3x/tg²4x=
x->0
Lim (x*3x)/(4x)²=3/16
x->0
заменяем бесконечно малые величины эквивалентными