Lim x-> ∞ (2x^2+6x-5)/(5x^2-x-1)
Ответы
Числитель и знаменатель разделим на x²:
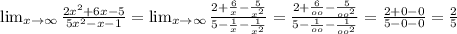
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Популярные вопросы
- За год все цены акций автомобильного предприятия превысились в 2,4 раза. сколько...
2 - Выполните вычисления в microsoft excel: цена 1 куб. метра леса в январе - n долларов....
1 - Составить 5 предложений на одну любую тему с не (не сложные, а для 6 класса)...
1 - Вроссии каждый человек потребляет ежедневно в среднем около 440 граммов причем...
2 - Объем куба равен 1000 дм2. определить длину его ребра....
3 - Вычисли 10105*3+3020*4 2909*2+1008*30 , 20500*3-12015*6 9600*40-1232*4...
1 - Стрех участков земли собрали 156ц картофеля. с первого и второго участков картофеля...
1 - Переведите на язык: 1. я не читал никаких книг этого писателя. 2. если что-нибудь...
2 - Известно что тепловодность газов меньше чем жидкостей и твердых тел. объясните...
2 - Творческая работа на окружающий мир на тему растения которые выведенные людьми...
3