Квадратное уравнение ax^2+bx+c=0 имеет ненулевые корни x_1 и x_2. Запишите квадратное уравнение с корнями 1/x_1 и 1/x_1 (укажите ограничения на коэффициенты a, b, `c).
Другие вопросы по теме Алгебра
Популярные вопросы
- Почему клетки столбчатой ткани имеют большее колличество хлоропластов,...
3 - Кому нужны щетинки для передвежения...
1 - Какие графические ассоциации со словами открытость, честность...
3 - Задать общий вопрос. 1. - they are doctors. ? 2. they have dot...
2 - 0,9 от 30% числа k равна 5,4. найдите число к...
1 - 25 центнеров 30 кг сколько это кг? 5 центнеров 70 кг сколько...
1 - Вдруг я остановился, пораженный звуками, каких до этого никогда...
3 - Функция задана формулой y=5x+21.определите значение y,если x=-3...
2 - Апочему позеленевшие клубни картофеля нельзя употреблять в пищу...
2 - Каким образовано слово дружинник...
2
В квадратном уравнение , которое имеет корни, обратные корням
, которое имеет корни, обратные корням
квадратного уравнения , меняются местами коэффициенты
, меняются местами коэффициенты  и
и  ,
,
причём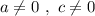 .
.
Запишем данное уравнение в более удобном виде:
ax^2+bx+c=0; (предполагается, что а=/=0)
Теорема Виета:
x1*x2=c/a,
x1+x2=-b/a.
Новое уравнение ищем в виде:
Ax^2+Bx+C=0
Опять Виет: (при условии, что с=/=0)
C/A=1/x1*1/x2=1/(x1*x2)=a/c, отсюда C=(a/c)*A
-B/A=1/x1+1/x2=(x2+x1)/(x1*x2)=(-b/a)/(c/a)=-b/c, отсюда B=(b/c)*A
Итак, Ax^2+(b/c)*Ax+(a/c)*A=0, и окончательно:
cx^2+bx+a=0