Кусок мыла имеет форму параллелепипеда. после 7 дней использования все его размеры уменьшились вдвое. на сколько дней ещё хватит этого мыла?

После 7 дней использования получился параллелепипед, которому подобен цельный кусок мыла (т.к. все стороны уменьшились в 2 раза), при этом коэффициент подобия k=2.

У подобных многогранников объёмы относятся, как .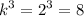

Пусть объём мыла, после 7 дней составляет Х куб. ед. Тогда объём цельного мыла составлял 8Х куб. ед.

Значит, за 7 дней потратилось 8Х-Х=7Х куб. ед. мыла.  

За 1 день - 7Х:7 = Х куб. ед.

Получается, что оставшийся кусок, объёмом Х куб. ед. потратится за 1 день.

ответ: один.