1. Алгебра
  2. Кто знает ответ на простой

Кто знает ответ на простой вопрос? Есть простая задача. Упростить выражение: при a>=4

Очевидно что выражение принимает следующий вид:

После сокращения квадратов и второй степени мы имеем:

После чего у меня получается: 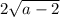2 \sqrt{a-2}
Но ответ гласит: 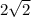2\sqrt{2}
Кто знает почему меняем знак перед вторым выражением, имея: = 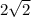2\sqrt{2}
??


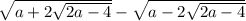
\sqrt{a+2\sqrt{2a-4}} - \sqrt{a-2\sqrt{2a-4}}
\sqrt(\sqrt{2} + \sqrt{a-2} )^{2} } - \sqrt(\sqrt{2} - \sqrt{a-2} )^{2} }
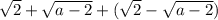
\sqrt{2} + \sqrt{a-2} - (\sqrt{2} - \sqrt{a-2} )
\sqrt{2} + \sqrt{a-2} + (\sqrt{2} - \sqrt{a-2})

Джеси99 Джеси99    2   02.04.2021 20:43    0

Ответы
kiraganziy kiraganziy  02.05.2021 20:48

\sqrt{a + 2 \sqrt{2a - 4} } - \sqrt{a - 2 \sqrt{2a - 4} } = \sqrt{( \sqrt{2} + \sqrt{a - 2}) {}^{2} } - \sqrt{( \sqrt{2} - \sqrt{a - 2}) {}^{2} } = | \sqrt{2} + \sqrt{a - 2} | - | \sqrt{2} - \sqrt{a - 2} |

Понятно, что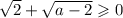 \sqrt{2}+\sqrt{a-2} \geqslant 0 так как корни всегда положительны, а вот с разностью корней может быть проблема.

За условием, а ≥ 4, тогда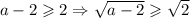 a - 2 \geqslant 2 \Rightarrow \sqrt{a-2} \geqslant \sqrt{2}. Следовательно 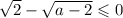\sqrt{2} - \sqrt{a-2} \leqslant 0. Тогда модуль открываем со знаком минус:

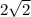\sqrt{2} + \sqrt{a - 2} - ( - (\sqrt{2} - \sqrt{a - 2} )) = \sqrt{2} + \sqrt{a - 2} + \sqrt{2} - \sqrt{a - 2} = 2 \sqrt{2}

ответ: 2\sqrt{2}.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
камкозавра камкозавра  16.05.2021 22:23
Просто напишите ответырисовать ничего не надо и только ВАРИАНТ б​...
брат2006кирилл брат2006кирилл  16.05.2021 22:23
РИСОВАТЬ НЕ НАДО ПРОСТО НАПИСАТЬ ОТВЕТ ​...
Alex90111 Alex90111  16.05.2021 22:24
100-у²=0 36-12х+х²=0 х+6 х-7 – - – 2 7...
18larina18 18larina18  16.05.2021 22:27
Решите уравнения:а) ; (8 Б.)б) . (8 Б.)БОНУС (づ｡◕‿‿◕｡)づ (24 Б.)Награда по умолчанию: (8 + 8 + БОНУС). Награда за лучший ответ: (40 + 50%).Только ответ с ЯСНЫМ решением...
chelovek70 chelovek70  16.05.2021 22:27
9. при яких значення а рівняння має один корінь ?​...
Наська0123 Наська0123  10.08.2019 22:20
1) постройте графики функции в одной системе координат. а)y=-0.2x б) y=4 2) проходит ли график функции y=-2x+4 через точку c (20; -36)? вот тут не одним словом да/нет...
anasasiyakoval anasasiyakoval  10.08.2019 22:20
Какая из данных точек не лежит на прямой заданной уравнением х+5у-3=0: 1)(13; -2) ; 1) ; 2) 4)(3; 5)...
AiratAitov AiratAitov  04.08.2019 02:20
Допишите к числам 12, 21, 36 еще семь любых чисел, так чтобы наибольший общий делитель из написанных чисел встречался среди этих чисел и чтобы наименьшее общее куратное...
ведитеник ведитеник  04.08.2019 02:20
Одна сторона прямоугольника равна a см ,а другая 4 см. составьте формулу зависимости площади прямоугольника от a....
dbnzgh dbnzgh  04.08.2019 02:20
На p рублей купили 1 ,5 кг конфет.составьте формулу зависимости цены конфет c от p. вычислите цену конфет при p= 75, 90 и 150...

Популярные вопросы