кто-то может подробно ОБЪЯСНИТЬ, как это решать? номер 123 и 124. и нет, не просто ответом в две строки. я хочу понять.. почему как и что делать. в учебнике ничего нет.

128. В точке х=1 у=1 и х=0; у=1  указанные графики пересекаются,  и их значения равны, если х∈(1;+∞), то обе функции у=х^(√2) и у= x^π возрастают, поэтому оба графика на этом промежутке лежат выше графика возрастающей на всей области определения (-∞;+∞) линейной функции у=х. Почему? потому что большему значению аргумента возрастающей функции соответствует большее значение функции, и так как √2≈1.4>1; π≈3.14>1, то и значения этих функций будут больше значения функции у=х.

Если же х∈(0;1) - , то здесь наоборот, функции у=х^(√2) и у= x^π убывают, и по аналогии с разобранным выше, графики этих функций будут находиться ниже графика у=х.

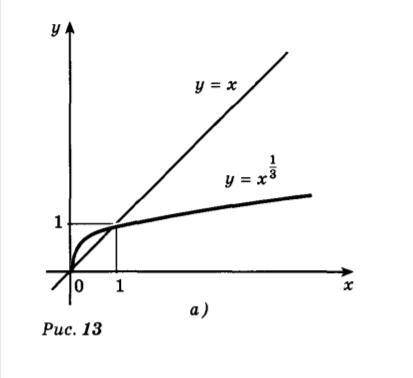
129. 1/π < 1; sin45°=√2/2 <1, здесь наоборот графики указанных функций  при х∈(0;1) лежат выше графика у =х, а при х∈(1;+∞), графики обеих  функций у=х^(√2) и у= x^π лежат ниже графика функции у=х, кстати, этому же правилу подчиняется и график, изображенный на рисунке. у=х^(1/3)