Корни уравнения x² + ax + b + 1=0 являются натуральными числами. Докажите, a² + b² - составное число.

Ответы

Andruha321 15.11.2020 13:50

Объяснение:

По теореме Виета

$(b+1)=x_{1} x_{2}\\a=-(x_{1}+ x_{2})$

Тогда

$a^{2}=(x_{1}+ x_{2})^{2}$

$b^{2} =(x_{1}x_{2}-1)^{2}$

$a^{2} +b^{2} =x_{1}^{2}+x_{2}^{2} +x_{1}^{2} x_{2}^{2} +1=(1+x_{1}^{2})(1+x_{2}^{2})$

Так как корни по условию натуральные, то число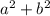 $a^{2} +b^{2}$ составное, что и требовалось доказать.

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра

vool23 26.09.2019 14:50

Решите уравнения: 1) log3(2x^2+x-1)=2 2) 7^5x-7^5x-2=6...

talyaarpaci 26.09.2019 14:50

Uniquehatter 26.09.2019 12:57

Kotik210 26.09.2019 13:00

evgen22region 26.09.2019 13:01

5х^2-2×^4+×^3 3mn+6m-4-2m 64k^2-(3k+1)^2решите...

Nadya0210 26.09.2019 13:01

миша1089 17.11.2020 16:01

При каких значениях x имеет смысл выражение: √-x^5 ...

vladbochilo 17.11.2020 16:01

26dura 17.11.2020 16:01

serotettonika 17.11.2020 16:02