Корни уравнения х^2-16х+q=0 относятся как 3: 5. найдите корни уравнения и свободный член.

Ответы

smchnc2004 04.08.2020 17:36

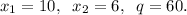ответ: $x_1=10, \;\; x_2=6, \;\; q=60.$ .

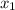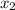По теореме Виета, мы знаем, что ( x_1 и x_2 - корни данного квадратного уравнения):

$x_1+x_2=16; \;\; x_1 \cdot x_2=q,$ при этом $3x_1=5x_2, \;\;\; \Rightarrow \;\;\; x_2=\frac{3}{5}x_1 .$

Подставляем:

$\displaystyle \left \{ {{x_1+\frac{3}{5}x_1=16} \atop {x_1 \cdot \frac{3}{5}x_1=q}} \right. ; \;\;\; \left \{ {{x_1=10} \atop {q=10 \cdot \frac{3}{5} \cdot 10}} \right. ; \;\;\; {\left \{ {{x_1=10} \atop {q=60}} \right.}.$

Ну и тогда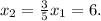 $x_2=\frac{3}{5} x_1=6.$

В ответ нужно записать:

$x_1=10, \;\; x_2=6, \;\; q=60.$ .

ПОКАЗАТЬ ОТВЕТЫ

koli17 04.08.2020 17:36

Корни уравнения 6 и 10; q=60.

Объяснение:

$x^{2} -16x+q=0;\\$

Данное уравнение квадратное . Пусть корни данного уравнения

$x{_1} , x{_2}$ . Тогда

$x{_1 }:x{_2}=3:5;$ и по теореме Виета

$\left \{ \begin{array}{lcl} {{x{_1} +x{_2}=16,} \\ {x{_1}*x{_2} =q.}} \end{array} \right.$

Составим и решим систему:

$\left \{ \begin{array}{lcl} {{\frac{x{_1}}{x{_2}}=\frac{3}{5} , } \\ {x{_1}+x{_2}=16;}} \end{array} \right.\Leftrightarrow \left \{ \begin{array}{lcl} {{x{_1}=\frac{3}{5} x{_2}}, \\ {\frac{3}{5} x{_2} +x{_2}=16;}} \end{array} \right.\Leftrightarrow\left \{ \begin{array}{lcl} {{x{_1} =\frac{3}{5}x{_2}, } \\ {3x{_2}+5x{_2} =80;}} \end{array} \Leftrightarrow\right.$

$\left \{ \begin{array}{lcl} {{x{_1}=\frac{3}{5} x{_2},} \\ {8x{_2}=80}} \end{array} \right.\Leftrightarrow\left \{ \begin{array}{lcl} {{x{_1}=\frac{3}{5} x{_2},} \\ {x{_2} =10;}} \end{array} \right.\Leftrightarrow \left \{ \begin{array}{lcl} {{x{_1} =6,} \\ {x{_2}=10.}} \end{array} \right.$