Корни квадратного уравнения 2019х² + ax + b = 0 — целые числа. докажите, что
дискриминант этого уравнения делится на 2019².​

Дискриминант извлекается из корня и с учетом того, что корни целые, то можно положить a = ±2019 и b = -2 * 2019

Следовательно,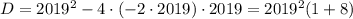 - делится на 2019²

Объяснение:

Докажем, что дискриминант этого уравнения делится на 2019².

По формуле Виета:

x₁+x₂= -a/2019

x₁•x₂=b/2019

По условию x₁ и x₂ целые числа, тогда a/2019 и b/2019 целые числа. Поэтому a=2019•c и b=2019•d, c∈Z и d∈Z.

Дискриминант имеет вид:

D=a²-4•2019•b=(2019•c)²-4•2019•(2019•d)=2019²•(c²-4•d)

что и доказывает утверждение.